Leire Mendieta-Echevarría1, María Ana Sáenz-Nuño2 y Eva María Rubio Alvir1
1 Departamento de Ingeniería de Construcción y Fabricación, Escuela Técnica Superior de Ingenieros Industriales, Universidad Nacional de Educación a Distancia (UNED)
2 Departamento de Ingeniería Mecánica, Instituto de Investigación Tecnológica (IIT), Universidad Pontificia Comillas
Resumen
El propósito de este artículo es comparar los algoritmos de cálculo de parámetros de rugosidad propios con otra herramienta software ampliamente utilizada y aceptada en este campo. Como antes de realizar cualquier tipo de cálculo de rugosidad es necesario aplicar una operación de filtrado para separar la rugosidad de la forma y ondulación de la superficie, también busca mostrar los efectos que tiene una operación de filtrado, en concreto, un filtro morfológico de superficie. Como se trata de un filtro bastante desconocido se muestra de forma gráfica la forma de aplicarlo.
En el estudio se incluyen únicamente los parámetros de rugosidad (3D), aunque se presenta algún ejemplo gráfico de filtrado morfológico de perfil (2D) con el fin de facilitar la comprensión de las operaciones involucradas y sus efectos.
Palabras clave: Rugosidad, calidad superficial (3D), metrología, filtro morfológico
Abstract
The purpose of this article is to compare proprietary roughness parameter calculation algorithms with another widely used and accepted software tool in this field. As before performing any kind of roughness calculation, it is necessary to apply a filtering operation to separate the roughness from the shape and waviness of the surface, it also aims to show the effects of a filtering operation, particularly a surface morphological filter. As this is a rather unknown filter, the way to apply it is shown graphically.
The study includes only areal roughness parameters (3D), although some graphical examples of profile morphological filtering (2D) are presented to facilitate understanding of the operations involved and their effects.
Keywords: Roughness, areal roughness, metrology,morphological filter
1. Introducción
La rugosidad superficial es una de las principales características utilizadas para describir el estado de una superficie y desempeña un papel fundamental en el comportamiento funcional de componentes mecánicos, especialmente en lo que respecta a fricción, desgaste, sellado y adherencia. Esta propiedad se cuantifica mediante parámetros estandarizados que permiten describir la topografía de una superficie de manera objetiva y reproducible. Con el fin de garantizar una caracterización uniforme y comparable a nivel internacional, dichos parámetros están definidos en normas técnicas como la UNE-EN ISO 25178-2:2023 [1], la cual establece los parámetros de textura superficial medidos sobre superficies tridimensionales.
Antes de calcular los parámetros de rugosidad es necesario aplicar una operación de procesado de datos previa llamada filtrado, con la que hay tener un gran cuidado, ya que, puede cambiar completamente los datos con los que se calculan los parámetros de rugosidad. Si bien en el estudio se han calculado numerosos parámetros de rugosidad, en el presente documento se presentan únicamente 11 de los definidos en la norma UNE-EN ISO 25178-2:2023[1], por ser los más comúnmente utilizados en la industria o aquellos cuya sensibilidad a las operaciones de filtrado es más significativa.
El filtrado de los datos es una parte esencial de la metrología para poder quitar las características no deseadas en los datos. Estas características no deseadas pueden ser ruido, outliers (valores anómalos que se distancian considerablemente de la tendencia del resto de datos) o simplemente datos con longitudes de onda no interesantes para el análisis que se busca realizar.
El filtrado puede aplicarse en perfiles (2D) o superficies (3D) y la normativa está recogida en la norma ISO 16610. En el anexo 2 la Tabla 6 y Tabla 7 recogen los filtros y normativa existentes. La norma EN ISO 16610-1:2015 [2] realiza una clasificación entre los filtros de perfil y de superficie y posteriormente entre lineales, robustos y morfológicos. Los morfológicos, que son filtros algo menos conocidos, utilizan una forma geométrica como elemento estructurante para descartar información no relevante.
Las tablas 2 y 3 de la norma UNE-EN ISO 25178-3:2013[3] para el caso de la superficie (3D) y las tablas 3, 4 y 5 de la norma UNE-EN ISO 21920-3:2023 [4] para el caso de los perfiles (2D), muestran una relación que se recomienda seguir entre la distancia de muestreo utilizada en las adquisiciones, el índice de anidamiento del filtro utilizado y el diámetro de palpador utilizado en los casos de las superficies inspeccionadas por contacto. En este estudio no se han considerado estas tablas porque se buscaba mostrar la influencia que puede tener la elección de un filtro en los resultados de rugosidad.
Mediante este artículo se busca mostrar la comparación entre los resultados de los algoritmos de cálculo de parámetros de rugosidad para dos paquetes software diferentes, así como explicar los fundamentos de los filtros morfológicos y como pueden afectar a la evaluación de los parámetros de rugosidad de superficie. En particular, se analiza el filtro morfológico de superficie de esfera de cierre, el cual simula el comportamiento del contacto de un palpador con la superficie durante la adquisición de datos.
Para realizar el estudio se han seleccionado los tamaños de filtros de 4 µm, 25 µm y 100 µm. Todos los tamaños corresponden con tamaños de partículas normalizadas presentes en los lubricantes [5]. De todos los posibles tamaños se han seleccionado los tamaños de partículas de 25 µm y 100 µm por su influencia en los resultados de los parámetros de rugosidad y el de 4 µm debido a que coincide con un tamaño de diámetro de rugosímetros muy utilizado.
2. Definiciones básicas
En este apartado se recoge la información básica sobre los parámetros de rugosidad y filtros utilizados en el documento.
2.1. Parámetros de rugosidad
A continuación, se muestra una tabla con los parámetros de rugosidad de superficie seleccionadas para el análisis, junto con su unidad. Todos ellos se recogen en la norma UNE-EN ISO 25178-2:2023 [1] y las unidades de cada uno de ellos en la norma UNE-EN ISO 25178-3:2013 [3].
| Tipos de parámetros | Parámetros de superficie | Unidades |
|---|---|---|
| Parámetros de altura | Altura media cuadrática (Sq) | µm |
| Asimetría (Ssk ) | 1 | |
| Aplastamiento ( Sku) | 1 | |
| Altura máxima de pico (Sp ) | µm | |
| Profundidad máxima de hoyo ( Sv) | µm | |
| Altura máxima (Sz ) | µm | |
| Altura media aritmética (Sa ) | µm | |
| Parámetros híbridos | Gradiente cuadrático medio (Sdq) | rad |
| Proporción de área interfacial desarrollada (Sdr) | % | |
| Parámetros de área para superficies estratificadas | Tasa portante de las colinas (Smrk1) | % |
| Tasa portante de los valles (Smrk2) | % |
En el apartado 11.1 se muestra la descripción de cada uno de los parámetros de la Tabla 1, junto con su fórmula según la norma UNE-EN ISO 25178-2:2023 [1].
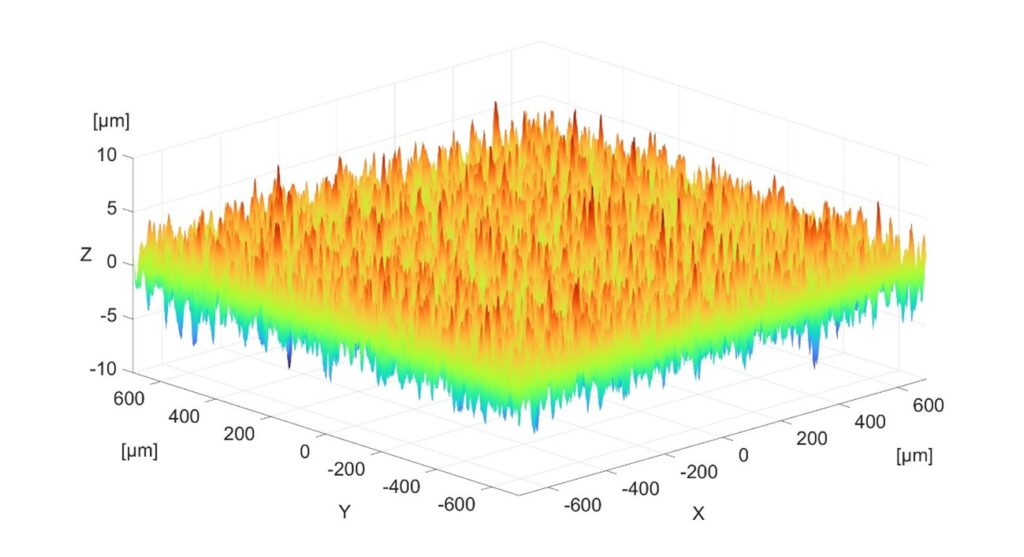
Para realizar el análisis se ha generado la nube de puntos que se muestra en la Figura 1. En la que entre los datos hay un distancia en horizontal de 0,2 µm en ambas direcciones.
Para realizar en análisis de como afecta un filtro morfológico a una superficie y a sus parámetros de rugosidad se utiliza la superficie de la Figura 2. En el apartado Appendix A de la referencia [5] se detalla el proceso de generación de la superficie.
2.2. Filtrado
El filtrado es un procesado de los datos que se realiza con el fin de quitar las características no deseadas de los datos. Se puede utilizar para filtrar ruido y outliers del resto de datos o para separar los datos de rugosidad, ondulación o forma.
2.2.1. Filtro morfológico
La norma EN ISO 16610-40:2015 [6] define el filtro morfológico como “operación morfológica que es monótonamente creciente e idempotente”. Pero explicándolo de forma más sencilla se podría decir que un filtro morfológico es un procesamiento de los datos que está formado por las operaciones de dilatación y erosión, que utiliza una forma geométrica como elemento estructurante para descartar información no relevante.
Se ha seleccionado un filtro de superficie morfológico de esfera de cierre (FAMCB: Filter Areal Morphological Close Ball), que es el mismo que se aplica de forma natural cuando un palpador de forma esférica entre en contacto con los puntos de la superficie a medir. En los valles pequeños, el palpador no llega al fondo, adquiriendo una profundidad ligeramente reducida. Sin embargo, puede medir correctamente todos los picos.
Los palpadores de rugosímetros más utilizados son los conos de ángulo de 90º terminados con una punta esférica de radio 2 µm o 5 µm.
Todavía no hay normativa existente para la aplicación de filtros morfológicos de superficie. Por esa razón, se ha seguido las recomendaciones de la norma de perfil (EN ISO 16610-41:2015[7]) para una forma de disco y se ha transformado a 3 dimensiones.
Este tipo de filtros están compuestos por dos operaciones básicas que son la dilatación y la erosión. En función del orden en el que se aplican estas operaciones los filtros pueden ser de cierre o de apertura. En los filtros de cierre se realiza en primer lugar la operación de dilatación y en segundo lugar la de erosión. En los de apertura se realiza primero la erosión y luego la dilatación.
La operación de dilatación aumenta la altura del conjunto de entrada y la de erosión la reduce. Por si solas no pueden considerarse un filtro morfológico, ya que, una de las condiciones para que se considere que es un filtro morfológico es que sea idempotente. Un filtro es idempotente cuando si se aplica el mismo tamaño de filtro sobre el mismo conjunto de datos da el mismo resultado independientemente de cuantas veces se aplique el filtro.
Los filtros de apertura provocan un efecto sobre los picos del perfil o superficie y los de cierre sobre los valles. Se podría considerar que son filtros direccionales, ya que solo atenúan los datos en una dirección.
En la Figura 3 se muestra un ejemplo de aplicación de un filtro de apertura y otro de cierre sobre el mismo perfil. Como se observa gráficamente el perfil resultante de aplicar el filtro de cierre solo tiene influencia sobre los valles y el de apertura sobre los picos.
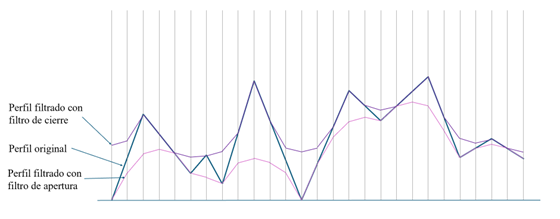
Este tipo de filtros presentan el efecto de borde para los perfiles o superficies abiertas, pero no para las cerradas. Explicar perfil superficie cerrada/abierta y efecto de borde. Este efecto se muestra en los extremos de los datos con una alteración de la forma del perfil o superficie.
Cuanto mayor es el tamaño del filtro utilizado mayor será el efecto de borde producido en los datos. En el caso de los perfiles hay técnicas para la compensación de estos efectos, que se definen en la norma UNE-EN ISO 16610-28:2018 [9]. Como para las superficies no existe ninguna técnica de compensación de estos efectos se ha filtrado una superficie mayor de la que se utiliza para los cálculos, con el fin de desechar los datos afectados por este efecto.
A continuación, se muestra de forma gráfica la aplicación de las operaciones de dilatación y de erosión para un filtro morfológico de perfil de disco de cierre, utilizando un disco como elemento filtrante.
En las siguientes figuras dm tiene el significado distancia de muestreo, que es la distancia que hay entre las líneas verticales de los gráficos. Aunque en los siguientes gráficos el perfil adquirido se muestre en forma de línea, cabe destacar que solo hay datos en los puntos coincidentes con las líneas verticales y, por tanto, solo se aplica el filtro a esos puntos.
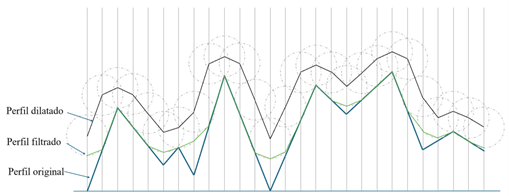
En las Figura 4 y Figura 5 se muestra la operación de dilatación de un perfil para dos tamaños de filtros diferentes. Para aplicar esta operación ha de colocarse el centro de un disco del mismo diámetro que el del filtro, en cada dato que haya en el perfil, es decir, en los lugares que coincida con la línea vertical. Con el exterior del disco que mayor altura tenga en cada una de las líneas verticales se compone el perfil dilatado.
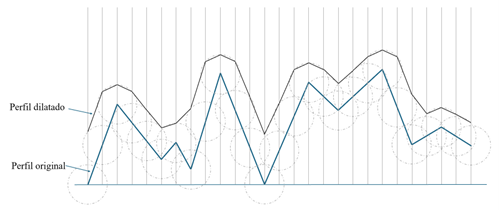
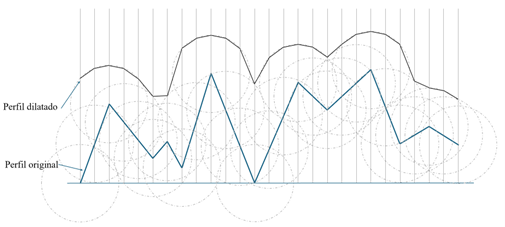
Se observa que en el la Figura 5 hay una variación mucho mayor en los valles del perfil inicial y del dilatado que en la Figura 4.
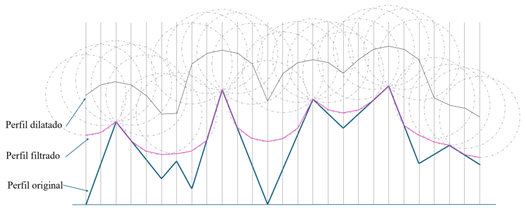
En las Figura 6 y Figura 7 se muestra la operación de erosión realizado sobre un perfil previamente dilatado. Para aplicar esta operación ha de colocarse el centro de un disco del mismo diámetro que el del filtro, en cada dato que haya en el perfil dilatado, es decir, en los lugares que coincida con la línea vertical. Con el exterior del disco que menor altura tenga en cada una de las líneas verticales se compone el perfil filtrado.
En la siguiente figura se muestra un gráfico comparativo del filtrado de un perfil con distintos tamaños.
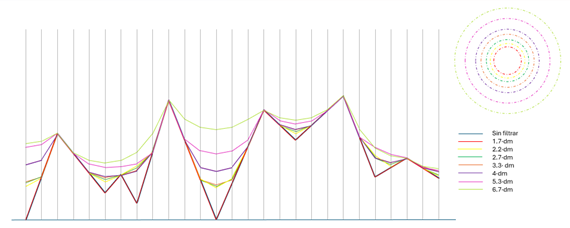
Aunque sería deseable mostrar el efecto del filtro de 4 µm, 25 µm y 100 µm de forma gráfica, no se apreciaría de forma gráfica la forma en la que actúan debido a la gran diferencia entre en tamaño del filtro y la distancia de muestreo.
Comparando los perfiles obtenidos con del filtrado, se observa una gran diferencia entre los perfiles resultantes para los diversos tamaños. Se aprecia que el tamaño de filtro 1,7·dm no ha realizado ninguna acción de filtrado debido a que no llega a un tamaño mínimo necesario. Esta gran diferencia entre los perfiles filtrados hace que haya que tener un cuidado especial al seleccionar el tamaño de filtro a utilizar, ya que, el perfil resultante puede cambiar completamente.
Para este estudio se ha utilizado una forma esférica como elemento filtrante para la superficie, pero podría realizarse el filtrado con otras formas como puede ser un plano. Aunque en estos momentos no hay ninguna norma publicada para realizar el filtrado morfológico de superficie, se ha consultado la norma EN ISO 11610-41:2015 [7], que es la norma que define los filtros morfológicos de perfil. Esta norma presenta los segmentos planos y los discos como elementos o formas filtrantes. Para aplicar el filtro en una superficie, se ha transformado el filtro de perfil de disco de cierre en un filtro morfológico de superficie de esfera de cierre, por la similitud entre ambas formas. Este tipo de filtro simula el mismo efecto que puede provocar un palpador sobre una superficie.
A la hora de escoger el tamaño del filtro hay que tener cuidado, ya que un filtro demasiado pequeño como ocurre en el caso de 1,7·dm no se realiza ningún tipo de filtrado. Y con un tamaño de filtro demasiado grande, 6,7·dm respecto de la muestra de datos a filtrar, el perfil puede cambiar completamente.
En la Figura 9 se muestra una captura de una simulación creada con Genially [10]. que muestra la aplicación del filtrado morfológico de perfil de disco de cierre, mediante sus dos operaciones básicas de dilatación y erosión.

3. Metodología
El siguiente es el diagrama de flujo que se ha seguido, comenzando con la generación de las superficies, seguido de la programación en Matlab 2024B [11] de los filtros y de los parámetros y finalizando con la recolección, visualización y comparación de los resultados.
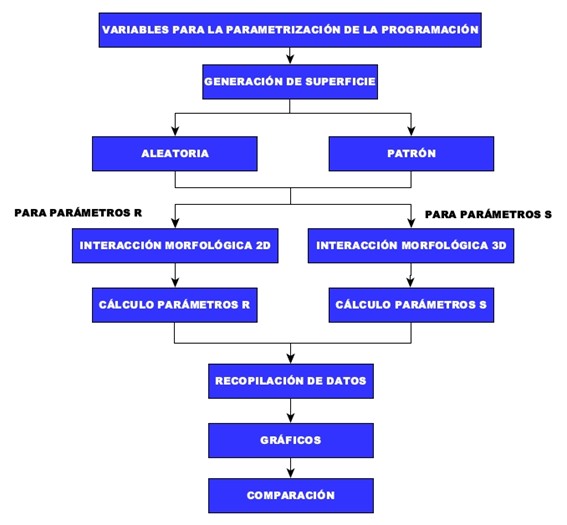
Aunque en este documento no se detallen todos los resultados de la investigación realizada, en la publicación de la referencia [5], se recoge la metodología e investigación completa realizada.
4. Resultados
4. 1. Resultados del software desarrollado
La Tabla 2 muestra los resultados de rugosidad superficial para la superficie sin filtrar y para la filtrada con los filtros morfológicos de cierre de 4µm, 25 µm y 100 µm.
| Parámetro | Sin filtrar | 4 µm | 25 µm | 100 µm |
|---|---|---|---|---|
| Sq [µm] | 1.6825 | 1.6811 | 1.5426 | 1.1109 |
| Ssk | -0.0056 | -0.0046 | 0.1227 | 0.3102 |
| Sku | 2.9573 | 2.9568 | 2.9522 | 3.2732 |
| Sp [µm] | 7.5584 | 7.5551 | 7.3200 | 6.2478 |
| Sy [µm] | 6.6769 | 6.6641 | 5.5356 | 3.9236 |
| Sz [µm] | 14.2354 | 14.2190 | 12.8556 | 9.9236 |
| Sa [µm] | 1.3458 | 1.3447 | 1.2353 | 0.8794 |
| Sdq [rad] | 0.4304 | 0.4259 | 0.3315 | 0.1690 |
| Sdr [%] | 8.6407 | 8.4735 | 5.2451 | 1.4130 |
| Smrk1 [%] | 9.5198 | 9.5227 | 10.1207 | 11.6327 |
| Smrk2 [%] | 90.0966 | 90.1033 | 90.8333 | 91.1754 |
Se observa que resultados para la superficie sin filtrar y la filtrada con el tamaño de 4 µm son muy similares.
En la tabla superior se observa que el parámetro que más se ve afectado por el filtrado es el parámetro Sdr. En la muestra inicial tiene un valor de 8,640 7 % y en la del filtro de 100 µm se reduce hasta 1,4130 %. Como este parámetro muestra la relación que hay entre la superficie interfacial y la superficie proyectada, al reducir los valles de la superficie con el filtrado, se reduce la superficie interfacial y aunque la superficie proyectada siga siendo la misma, el valor de dicho parámetro se ve reducido.
Otro parámetro que cambia notablemente es Sdq, que comienza siendo 0,430 4 rad y termina siendo 0,169 0 rad. Tal y como se muestra en la ecuación (8) su cálculo está basado en el gradiente de la superficie. Al aplicar tamaños grandes del filtro, el tamaño de los valles se reduce significativamente y, por tanto, el gradiente de la superficie también.
El parámetro Sv, parámetro que evalúa la profundidad de los valles, se reduce casi a la mitad de su tamaño inicial, en la superficie sin filtrar tiene un valor de 6,676 9 µm y en la superficie filtrada con el filtro de 100 µm. Aunque se haya comentado con anterioridad que el filtro de cierre afecta a los valles y el parámetro Sp sea un parámetro referido a la altura de los picos, aunque los picos no cambien esté parámetro se ve afectado por el filtrado. El parámetro Sp se calcula con la altura que hay entre el pico más alto y el plano medio de la superficie, a pesar de que el pico más alto de la superficie no se vea afectado, el resto de la superficie evoluciona significativamente, reduciendo los valles y provocando que el plano medio se sitúe más elevado en el eje Z y, por tanto, haya una altura menor entre el plano medio y el pico más alto. El parámetro de altura máxima, Sz, también se ve reducido con el filtrado teniendo un valor de 14,235 4 µm en la nube de puntos inicial y 9,923 6 µm.
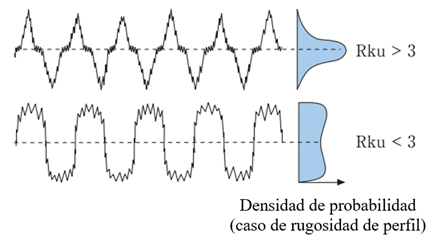
Se observa que el parámetro Sku aumenta con el aumento del tamaño del filtro, partiendo de un valor inicial de 2,957 3 y alcanzando un valor de 3,273 2 para el filtro de 100 µm, además de que supera el valor de 3. En el caso de este parámetro ese valor es muy significativo, ya que, este parámetro hace referencia a la distribución de los datos que tiene la superficie respecto al eje Z. Cuando tiene un valor de 3 la distribución de estos datos es normal, cuando es menor a 3 es uniforme y cuando es mayor a 3 es afilada.
Al igual que el parámetro de kurtosis, Ssk también aumenta con el filtrado. En este caso se observa un cambio de signo, ya que, comienza en -0,005 6 y alcanza un valor de 0,310 2. Este aumento del valor se debe al nivel de asimetría que hay en la distribución de alturas de la superficie.
Los parámetros Sa y Sq también se reducen de forma considerable con el filtrado. Sa parte de 1,345 8 µm y se reduce hasta 0,879 4 µm. El parámetro Sq varía desde 1,682 5 µm hasta 1,110 9 µm.
Los parámetros Smrk1 y Smrk2 aumentan ligeramente. Smrk1 tiene un valor de 9,5198 % en la superficie inicial y 11,632 7 % en la resultante del filtro de gran tamaño. Smrk2 va desde 90,096 6 % hasta 91,175 4 %.
En el artículo de la referencia [5] se muestran más efectos de los filtros morfológicos de perfil de cierre y superficie de cierre.
En las siguientes figuras se muestra la nube de puntos sin filtrar (Figura 11), la resultante del filtrado de 4 µm (Figura 12), la de 25 µm (Figura 13) y la de 100 µm (Figura 14).
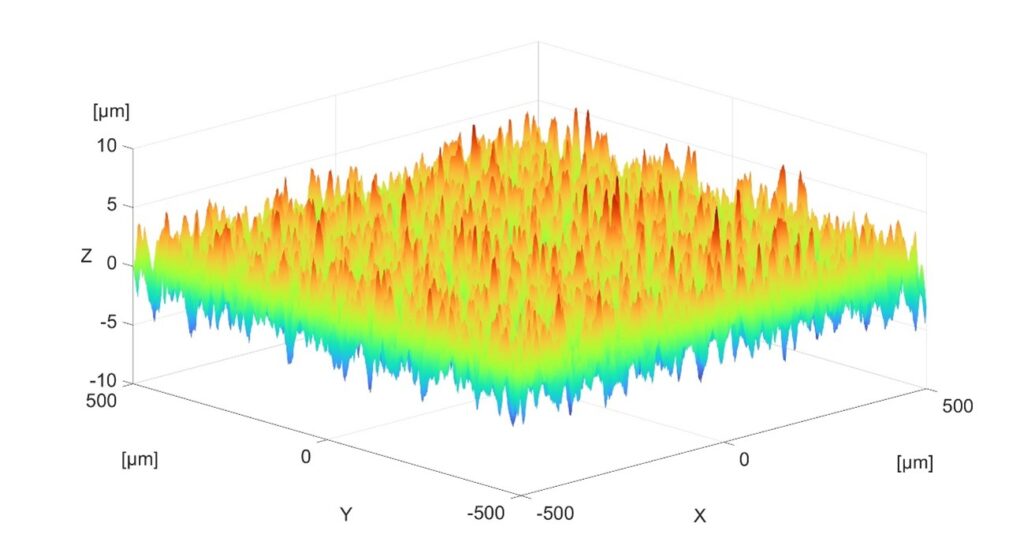
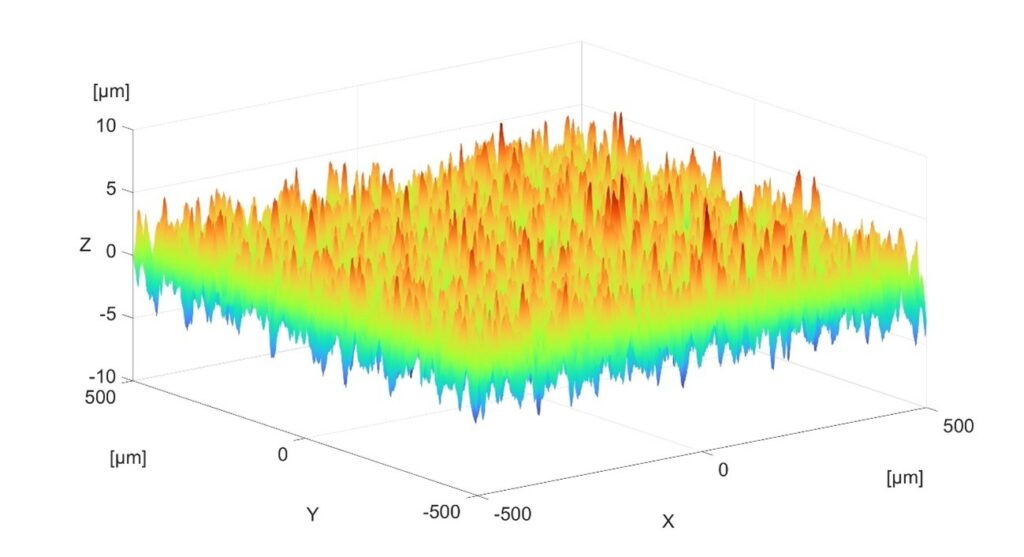
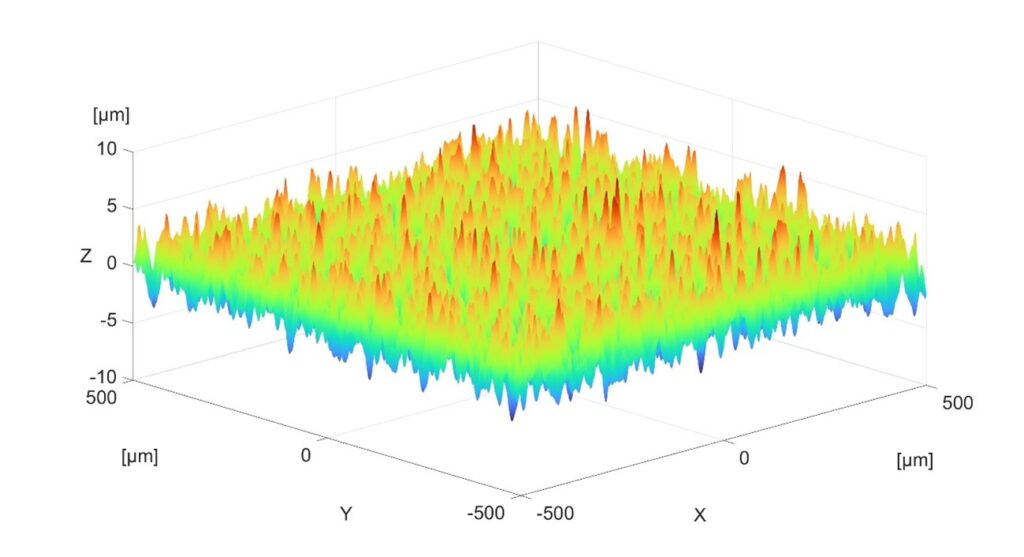
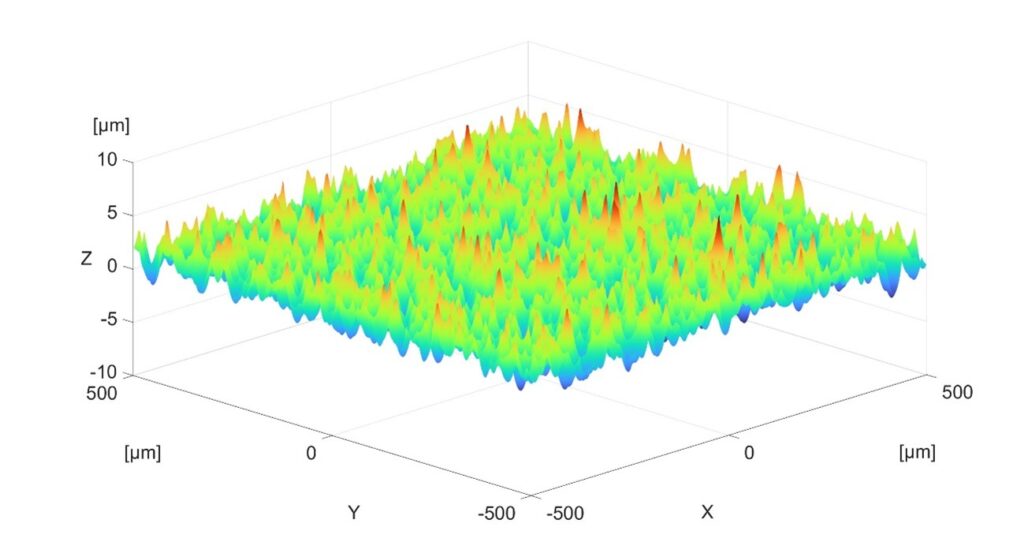
Comparando las tres superficies, la Figura 12 es muy similar a la Figura 11, en la Figura 13 se muestra un leve redondeo en los valles comparándola con la Figura 11. En la Figura 14 se observa una clara reducción de los valles de la superficie, que provoca una reducción en la amplitud que tiene la superficie en el eje Z, tal y como se aprecia en el parámetro Sz de la Tabla 2.
La curva de tasa portante proporciona información sobre la textura de la superficie. Como se muestra en la siguiente Figura 15, por cada altura horizontal muestra el porcentaje de puntos (o datos) que hay en la nube de puntos por encima de ese nivel de intersección.
En la siguiente gráfica se muestra la relación entre un trozo de la superficie original y la curva de material ratio para una altura de 1 µm en el eje Z. Todas las partes marcadas en azul están a una altura mayor de 1 µm y como se aprecia en el eje horizontal de la curva de material ratio son el 23,898 5 % de la superficie.
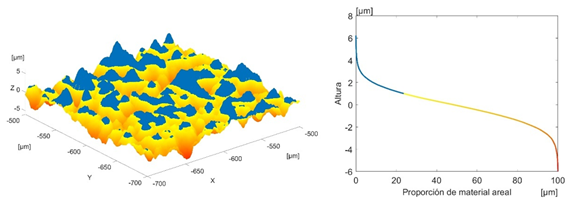
La Figura 16 muestra la curva de tasa portante para la superficie inicial y para las filtradas.
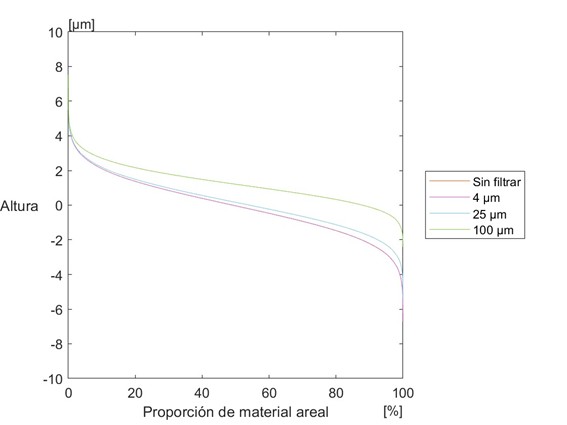
Como se aprecia en la Figura 16, la parte derecha de la curva se ve más afectada por el filtrado morfológico de cierre aplicado. Como se ha explicado con anterioridad la parte izquierda de la curva corresponde con los puntos más altos de la superficie y la derecha con los más bajos, es decir, con los valles. Por tanto, al utilizarse un filtrado de cierre, que es el que filtra los valles, se aprecia una mayor variación en la parte derecha de la curva.
En la curva de tasa portante se observa un solape completo entre la superficie original y la filtrada con el tamaño de 4 µm, una leve variación con el filtro de 25 µm y una gran variación con el de 100 µm, sobre todo en la parte derecha de la curva, la correspondiente a los valles.
4.2. Comparación de resultados con la herramienta Surfalize
Para demostrar la veracidad de los resultados obtenidos con el software de cálculo de rugosidad desarrollado, se han comparado los resultados con la herramienta de software libre Surfalize [12], que esta implementada en Python. En la siguiente tabla se recogen los resultados de los parámetros de rugosidad obtenidos con Surfalize [12].
Con el fin de que los algoritmos de cálculo sean comparables el filtro de utilizado las mismas nubes de puntos para realizar los cálculos.
| Parámetros | Sin filtrar | 4 µm | 25 µm | 100 µm |
|---|---|---|---|---|
| Sq [µm] | 1,682 5 | 1,681 1 | 1,542 6 | 1,110 9 |
| Ssk | -0,005 6 | -0,004 6 | 0,122 7 | 0,310 2 |
| Sku | 2,957 3 | 2,956 8 | 2,952 2 | 3,273 2 |
| Sp [µm] | 7,558 4 | 7,555 1 | 7,320 0 | 6,247 8 |
| Sv [µm] | 6,676 9 | 6,664 1 | 5,535 6 | 3,675 7 |
| Sz [µm] | 14,235 4 | 14,219 1 | 12,855 6 | 9,923 6 |
| Sa [µm] | 1,345 8 | 1,344 7 | 1,235 3 | 0,879 4 |
| Sdq[rad] | 0,432 2 | 0,427 8 | 0,332 1 | 0,169 3 |
| Sdr [%] | 8,687 3 | 8,520 0 | 5,289 2 | 1,454 1 |
| Smrk1 [%] | 9,160 7 | 9,164 0 | 9,729 6 | 11,170 7 |
| Smrk2 [%] | 90,467 9 | 90,478 7 | 91,221 4 | 91,578 4 |
En la siguiente tabla se muestra la variación porcentual entre los resultados de las dos herramientas analizadas. Los valores de la Tabla 4 se han calculado siguiendo la formula:
\(Variación= \left|\left(v_{surf}-v_{propia}\right)/max{\left(v_{surf},v_{propia}\right)}\right|\)
(1)
Siendo,
\(v_{surf}\) el valor del parámetro resultante del cálculo con el paquete Surfalize [12].
\(v_{propia}\) el valor del parámetro resultante del cálculo con la librería de desarrollo propio.
| Parámetros | Sin filtrar | 4 µm | 25 µm | 100 µm |
|---|---|---|---|---|
| Sq | 0,000 0 % | 0,000 0 % | 0,000 0 % | 0,000 0 % |
| Ssk | 0,000 0 % | 0,000 0 % | 0,000 0 % | 0,000 0 % |
| Sku | 0,000 0 % | 0,000 0 % | 0,000 0 % | 0,000 0 % |
| Sp | 0,000 0 % | 0,000 0 % | 0,000 0 % | 0,000 0 % |
| Sv | 0,000 0 % | 0,000 0 % | 0,000 0 % | 0,000 0 % |
| Sz | 0,000 0 % | 0,000 0 % | 0,000 0 % | 0,000 0 % |
| Sa | 0,000 0 % | 0,000 0 % | 0,000 0 % | 0,000 0 % |
| Sdq | 0,419 4 % | 0,460 8 % | 0,206 9 % | 0,167 6 % |
| Sdr | 0,536 8 % | 0,545 8 % | 0,833 5 % | 2,828 6 % |
| Smrk1 | 3,772 2 % | 3,766 8 % | 3,864 9 % | 3,971 8 % |
| Smrk2 | 0,410 5 % | 0,414 9 % | 0,425 5 % | 0,440 1 % |
Los resultados obtenidos para los parámetros de altura son exactamente iguales. Los parámetros Sdq y Smrk2 presentan una pequeña variación y los parámetros que tienen un mayor cambio son Smrk1 y Sdr, en concreto Smrk1. La diferencia entre los resultados del parámetro Smrk1 puede deberse al cálculo de la secante mínima de la curva de tasa portante, el parámetro Smrk2 también se ve afectado por este cálculo, pero al tener un valor aproximadamente 10 veces mayor tiene una variación porcentual mucho menor.
Al utilizar plataformas de cálculo diferentes puede generarse una pequeña variación entre los resultados debido al número de decimales utilizados en el cálculo.
5. Discusión
En la Figura 17 se muestra la variación porcentual de cada parámetro analizado para el software implementado.
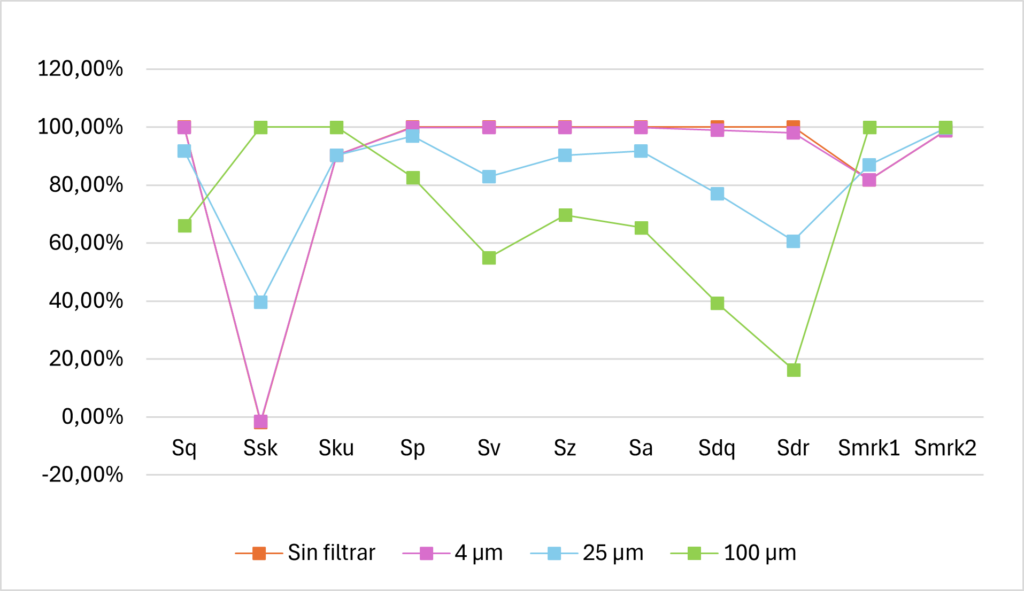
Comparando los resultados obtenidos se observa que entre los datos sin filtrar y los filtrados con el diámetro de 4 µm son muy similares, pero presentan una mayor variación para los tamaños de 25 µm y 100 µm.
Revisando el gráfico superior parece que el parámetro que presenta la mayor variación es Ssk, pero en realidad la variación no es tan grande en el gráfico se ve exagerada debido a que en ese parámetro hay un cambio de signo que exagera la variación real.
El siguiente parámetro que muestra más variación es el parámetro Sdr, que es en realidad el que más varía. Sdr se reduce hasta el 16,35 % de su valor inicial. Esto hace de Sdr un parámetro a tener en cuenta al aplicar cualquier tipo de filtrado, es un parámetro muy sensible y hay que tener precaución con el tamaño de filtro a utilizar.
Otro parámetro con gran variación es Sdq, que al igual que Sdr es un parámetro hibrido.
El parámetro Smrk2 es el que menor sensibilidad presenta ante el filtrado.
6. Conclusiones
Después del estudio realizado se sacan las siguientes conclusiones:
- Los datos obtenidos con las dos herramientas son similares, aunque presentan mayores variaciones en los parámetros Smrk1 y Sdr.
- Hay que tener un cuidado especial a la hora de seleccionar el tamaño de un filtro para cualquier cálculo, ya que como se aprecia a lo largo del artículo los resultados obtenidos pueden cambiar completamente.
- El tamaño del filtro a utilizar debe ser como mínimo del doble del tamaño de la distancia de muestreo, ya que, si el tamaño del filtro es menor no se realizará ningún tipo de acción de filtrado.
\(diámetro_{filtro} \geq 2\ \ast distancia_{muestreo}\)
(2)
- Si los datos se han adquirido con un sistema de palpado con contacto, para que haya una acción de filtrado el filtro debe ser mayor al palpador utilizado.
- Considerar el efecto de borde y adquirir una muestra de mayores dimensiones que la que se necesita analizar, ya que, los datos de los extremos se verán afectados y será necesario desecharlos.
- Por el efecto de borde no se recomienda usar filtros de gran tamaño en muestras pequeñas.
- En el procesado de los datos con el filtrado se observa que por la naturaleza de los cálculos necesarios para aplicar las operaciones de filtrado.
- Se debe tener cuidado con el tamaño del filtro seleccionado, ya que, la superficie o perfil resultante puede varían notablemente.
- Los parámetros híbridos son los más afectados por las operaciones de filtrado morfológico, en concreto el más afectado es el parámetro Sdr.
- Smrk2 presenta muy poca sensibilidad ante el filtrado.
- Se recomienda que el tamaño del filtro no exceda el 20% del tamaño de la muestra.
- En caso de utilizar filtros grandes se aconseja realizar el filtrado de forma iterativa, aplicando primero filtros más pequeños y finalmente el tamaño que se desea utilizar.
- Es conveniente que cuando un laboratorio se dedique a medir la rugosidad y quiera utilizar este tipo de filtro, una vez que tenga su equipo o procedimiento caracterizado calcule la incertidumbre asociada al filtrado.
7. Líneas futuras
Entre las siguientes líneas de investigación están:
- Terminar de implementar los algoritmos de cálculo para la evaluación de la rugosidad superficial detallados en la norma UNE-EN ISO 25178-2:2023 [1].
- Optimizar el algoritmo del filtro morfológico para reducir el tiempo de procesamiento.
- Implementar otros filtros de la norma UNE-EN ISO 16610 y comparar los resultados y tiempos de procesamiento de cada uno.
- Considerar la forma cónica que presentan los rugosímetros en el filtro morfológico. En este estudio solamente se ha considerado la punta esférica.
- Realizar un estudio estimando el impacto que puede tener el considerar el efecto de borde en los resultados.
8. Referencias
- UNE-EN ISO 25178-2:2023 Geometrical product specifications (GPS). Surface texture: Areal. Part 2: Terms, definitions and surface texture parameters. (ISO 25178-2:2021)
- EN ISO 16610-1:2015. Especificación geométrica de productos (GPS). Filtración. Parte 1: Perspectiva general y conceptos de básicos (ISO 16610-1:2015) (Ratificada por AENOR en julio de 2015.)
- UNE-EN ISO 25178-3:2013 Geometrical product specifications (GPS). Surface texture: Areal. Part 3: Specification operators. (ISO 25178-3:2012)
- UNE-EN ISO 21920-3:2023. Especificación geométrica de productos (GPS). Calidad superficial: Método del perfil. Parte 3: Operadores de especificación. (ISO 21920-3:2021)
- Mendieta-Echevarría, L., Sáenz-Nuño, M. A., & Rubio, E. M. (2025). Comparing the Effectiveness of R and S Roughness Parameters on Surfaces Lubricated with Standardized Nominal Particle Size Lubricants. Lubricants, 13(4), 148. https://doi.org/10.3390/lubricants13040148
- EN ISO 16610-40:2015 Geometrical product specifications (GPS) – Filtration – Part 40: Morphological profile filters: Basic concepts. (ISO 16610-40:2015) (Ratificada por AENOR en agosto de 2015.)
- EN ISO 16610-41:2015 Geometrical product specifications (GPS) – Filtration – Part 41: Morphological profile filters: Disk and horizontal line-segment filters. (ISO 16610-41:2015). (Ratificada por AENOR en septiembre de 2015.)
- Lingadurai, K; Shunmugam, M. S. Use of morphological closing filters for three-dimensional filtering of engineering surfaces. 2008. https://doi.org/10.1016/S0278-6125(05)80020-2
- UNE-EN ISO 16610-28:2018 Geometrical product specifications (GPS). Filtration. Part 28: Profile filters: End effects. (ISO 16610-28:2016)
- Genially, https://genially.com/
- MATLAB, https://es.mathworks.com/products/matlab.html
- F. Schell, C. Zwahr, A. F. Lasagni. Surfalize: A Python Library for Surface Topography and Roughness Analysis Designed for Periodic Surface Structures. Nanomaterials. 2024, 13, 1076., https://github.com/fredericjs/surfalize
- Olympus. Introduction to Surface Roughness Measurement. Roughness measurement guidebook. https://www.qualitymag.com/ext/resources/files/white_papers/Olympus/LEXT-Surface-Roughness.pdf
- UNE-EN ISO 16610-21:2013 Geometrical product specifications (GPS) Filtration. Part 21: Linear profile filters: Gaussian filters (ISO 16610-21:2011)
- EN ISO 16610-22:2015 Especificación geométrica de productos (GPS). Filtración. Parte 22: Filtros de perfil lineal: filtros de ranura ISO 16610-22:2015). (Ratificada por AENOR en septiembre de 2015.)
- EN ISO 16610-29:2015 Especificación geométrica de productos (GPS). Filtración. Parte 29: Filtros de perfil lineal: Ranuras onduladas (ISO 16610-29:2015) (Ratificada por AENOR en julio de 2015.)
- EN ISO 16610-49:2015 Especificación geométrica de productos (GPS). Filtración. Parte 49: Filtros de perfil morfológico: Técnicas de análisis para el espacio de las escalas. (ISO 16610-49:2015) (Ratificada por AENOR en agosto de 2015.)
- UNE-EN ISO 16610-31:2018 Especificación geométrica de productos (GPS) Filtración Parte 31: Filtros de perfil robustos: filtros de regresión gausianos (ISO 16610-31:2016)
- ISO/TR 16610-32:2023 Geometrical product specifications (GPS) — Filtration Part 32: Robust profile filters: Spline filters
- UNE-EN ISO 3274:1998 Especificación geométrica de productos (GPS) Calidad superficial: Método del perfil Características nominales de los instrumentos de contacto (palpador) (ISO 3274:1996)
- UNE-EN ISO 16610-61:2015 Especificación geométrica de productos (GPS). Filtración. Parte 61: Filtros superficiales lineales. Filtros Gaussianos (ISO 16610-61:2015)
- EN ISO 16610-71:2014 Especificación técnica de productos (GPS). Filtración. Parte 71: Filtros superficiales robustos: Filtros de regresión gaussianos (ISO 16610-71:2014)
9. Anexos
9.1. Anexo 1: Definiciones de los parámetros de rugosidad
Altura media cuadrática (Sq)
“El parámetro de altura media cuadrática es la raíz cuadrada de la media de los cuadrados de los valores de las ordenadas de la superficie de escala limitada. A veces, se denomina altura RMS.” [1]
\(S_{q}=\sqrt{\frac{1}{A}\iint_{\widetilde{A}}z^2\left(x,y\right)dxdy}\)
(3)
Asimetría (Ssk)
“El parámetro de asimetría es el cociente entre el valor cúbico medio de los valores de las ordenadas de la superficie de escala limitada y el cubo de Sq.” [1]
\(S_{sk}=\frac{1}{AS_q^3}\iint_{\widetilde{A}}z^{3}\left(x,y\right)dxdy\)
(4)
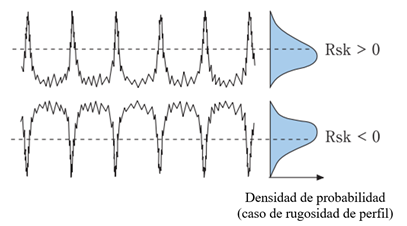
El parámetro de asimetría cuantifica la distribución de los datos en altura. Como se aprecia en la Figura 18 cuando el parámetro tiene un valor positivo la mayor parte de los datos se sitúan por debajo de la línea media y cuando es negativo sobre ella. Cuando el parámetro es 0 la distribución es normal [13].
Aplastamiento (Sku)
“El parámetro de aplastamiento es el cociente entre el valor cuadrático medio de los valores de las ordenadas de la superficie de escala limitada y la cuarta potencia de Sq.” [1]
\(S_{ku}=\frac{1}{AS_q^4}\iint_{\widetilde{A}}z^{4}\left(x,y\right)dxdy\)
(5)
Este parámetro está relacionado con la geometría de los picos y los valles. Como se aprecia en la Figura 19 cuando el parámetro de aplastamiento es mayor a 3 la distribución es afilada, cuando es 3 la distribución es normal y cuando es menor a 3 es uniforme [13].
Altura máxima de pico (Sp)
“El parámetro de altura de pico máxima es el mayor valor de altura de pico de la superficie de escala limitada.” [1]
Profundidad máxima de hoyo (Sv)
“El parámetro de profundidad máxima de hoyo es el mayor valor de profundidad de hoyo de la superficie de escala limitada. Sv es siempre una cantidad positiva, ya que la superficie de referencia es siempre superior a al hoyo más profundo.” [1]
Altura máxima (Sz)
“El parámetro de altura máxima es la suma del valor de la altura máxima de pico y del valor de profundidad máxima de hoyo de la superficie de escala limitada.” [1]
\(S_{z}=S_{p}+S_{v}\)
(6)
Altura media aritmética (Sa)
“El parámetro de altura media aritmética es la media de los valores absolutos de las ordenadas de la superficie de escala limitada.” [1]
\(S_{a}=\frac{1}{A}\iint_{\widetilde{A}}\left |z\left(x,y\right)\right |dxdy\)
(7)
Gradiente cuadrático medio (Sdq)
“El parámetro del gradiente cuadrático medio es la raíz cuadrada de la media de los cuadrados del gradiente de la superficie de escala limitada.” [1]
\(S_{dq}=\sqrt{\frac{1}{A}\iint_{\widetilde{A}}\left[\left(\frac{\partial z\left(x,y\right)}{\partial x}\right)^2+\left(\frac{\partial z\left(x,y\right)}{\partial y}\right)^2\right]dxdy}\)
(8)
Proporción de área interfacial desarrollada (Sdr)
“El parámetro de la proporción de área interfacial desarrollada es la relación del incremento del área interfacial de la superficie de escala limitada sobre el área de evaluación.” [1]
\(S_{dq}=\frac{1}{A}\iint_{\widetilde{A}}\left ( \sqrt{\left [ 1+ \left(\frac{\partial z\left(x,y\right)}{\partial x}\right)^2+\left(\frac{\partial z\left(x,y\right)}{\partial y}\right)^2\right ]-1} \right )dxdy\)
(9)
Aunque la formula anterior muestre la forma ideal de calcularlo, está formula solo puede utilizarse en los casos en los que la superficie sea ideal o perfecta. Como la superficie no suele ser ideal es necesario calcular la superficie interfacial siguiendo la siguiente formula, en la que se calcula la superficie por cada avance en X(ΔX) e Y(ΔY ).
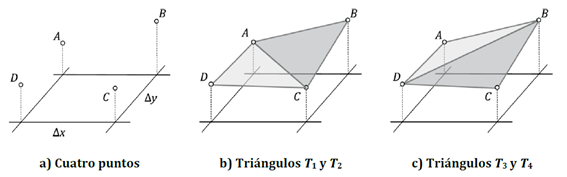
\(a_{i,j}=\frac{1}{2}\left[\left(\frac{1}{2}\left|\vec{BA}\times\vec{BC}\right|+\frac{1}{2}\left|\vec{DA}\times\vec{DC}\right|\right)+\left(\frac{1}{2}\left|\vec{AB}\times\vec{AD}\right|+\frac{1}{2}\left|\vec{CB}\times\vec{CD}\right|\right)\right]\)
(9)
En la Figura 20 se muestra la descomposición en triángulos que se realiza de cada uno de los cuadrilateros de puntos de la superficie para poder calcular la superficie interfacial.
Tasa portante de las colinas (Smrk1)
“El parámetro tasa portante de las colinas es la tasa portante en la línea de intersección que separa las colinas salientes de la superficie del núcleo.” [1]
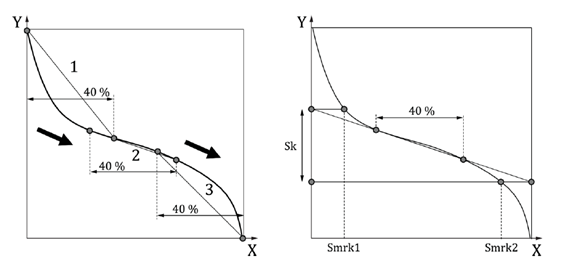
En la Figura 21 se muestra una representación gráfica de los parámetros Smrk1 y Smrk2 y de la forma en la que se obtienen. En primer lugar, hay que obtener la curva de tasa portante, y en esta la secante mínima utilizando el 40 % de los datos de la curva. Los valores en altura que tiene la línea que se ajusta a la secante mínima para el 0 % y 100 % del eje horizontal, definen los límites de Sk. Smrk1 es el valor de la proporción de material areal (eje horizontal) que coincide con el límite superior de Sk y Smrk2 el que coincide con el límite inferior de Sk.
Tasa portante de los valles (Smrk2)
“El parámetro tasa portante de los valles es la tasa portante en la línea de intersección que separa los valles que sobresalen de la superficie del núcleo.” [1]
9.2. Anexo 2: Filtros de la Norma ISO 16610
En la siguiente tabla de elaboración propia se recoge la denominación de las siglas de los filtros de en la norma EN ISO 16610-1:2015 [2].
| NIVEL (ORDEN SÍMBOLOS) | SÍMBOLO | NOMBRE |
|---|---|---|
| 1 | F | Filtro |
| 2 | A | Superficie/área (3D) |
| 2 | P | Perfil (2D) |
| 3 | L | Lineal |
| 3 | M | Morfológico |
| 3 | R | Robusto |
| 4 | 2RC* | Paso bajo de segundo orden RC |
| 4 | AB | Esfera alterna |
| 4 | AD | Disco alterno |
| 4 | AH | Segmento horizontal alterno |
| 4 | CB | Esfera de cierre |
| 4 | CD | Disco de cierre |
| 4 | CH | Segmento horizontal de cierre |
| 4 | G | Gaussiano |
| 4 | OB | Esfera de apertura |
| 4 | OD | Disco de apertura |
| 4 | OH | Segmento horizontal de apertura |
| 4 | S | Spline |
| 4 | SW | Spline wavelet |
* El filtro 2RC pertenece a un caso especial y no tiene el nivel 3 de la nomenclatura.
En la Tabla 6 se recoge una clasificación de los filtros de perfil y en la Tabla 7 los de superficie.
| CATEGORIA | SÍMBOLO | SIGLAS | NOMBRE | PARTE DE LA NORMA |
|---|---|---|---|---|
| FPL (Lineal) | G | FPLG | Gaussiano | 16610-21:2013 [14] |
| S | FPLS | Spline | 16610-22:2015 [15] | |
| SW | FPLSW | Spline wavelet | 16610-29:2015 [16] | |
| FPM (Morfológico) | CD | FPMCD | Morfológico de disco de cierre | 16610-41:2015 [7] |
| CH | FPMCH | Morfológico de segmento horizontal de cierre | 16610-41:2015 [7] | |
| OD | FPMOD | Morfológico de disco de apertura | 16610-41:2015 [7] | |
| OH | FPMOH | Morfológico de segmento horizontal de apertura | 16610-41:2015 [7] | |
| AD | FPMAD | Morfológico de disco alternos | 16610-49:2015 [17] | |
| AH | FPMAH | Morfológico de segmento horizontal alternos | 16610-49:2015 [17] | |
| FPR (Robusto) | G | FPRG | Robusto gaussiano | 16610-31:2018 [18] |
| S | FPRS | Robusto spline | 16610-32:2023 [19] | |
| FP(Especial) | 2RC | FP2RC | Paso bajo de segundo orden RC | 3274:1998 [20] |
| CATEGORIA | SÍMBOLO | SIGLAS | NOMBRE | PARTE DE LA NORMA |
| FAL (Lineal) | G | FALG | Gaussiano | 16610-61:2015 [21] |
| S | FALS | Spline | 16610-62 | |
| SW | FALSW | Spline wavelet | 16610-69 | |
| FAM (Morfológico) | CB | FAMCB | Morfológico de esfera de cierre | 16610-81 |
| CH | FAMCH | Morfológico de segmento horizontal de cierre | 16610-81 | |
| OB | FAMOB | Morfológico de esfera de apertura | 16610-81 | |
| OH | FAMOH | Morfológico de segmento horizontal de apertura | 16610-81 | |
| AB | FAMAB | Morfológico de esfera alternos | 16610-89 | |
| AH | FAMAH | Morfológico de segmento horizontal alternos | 16610-89 | |
| FAR (Robusto) | G | FARG | Robusto gaussiano | 16610-71:2014 [22] |
| S | FARS | Robusto spline | 16610-72 |
Las normas marcadas en naranja no se han desarrollado o publicado, pero en la norma EN ISO 16610-1:2015 [2] aparece que tienen el número de la norma reservado.










Comentarios