Aplicación de las técnicas Bootstrap en Metrología

Miguel Angel López Díaz
Facultad de Ciencias, UAEMEX.

NOTA: Artículo publicado en la revista editada por la Asociación Mexicana de Metrología A. C. (AMMAC.MX)  

Preliminares

El termino Bootstrap proviene de la expresión “pulling oneself up by one’s bootstrap” que puede traducirse como levantar uno mismo sus botas, y que en inglés hace referencia a hacer algo difícil sin ayuda externa.

El método Bootstrap tiene una historia fascinante que surge en el contexto del desarrollo de las técnicas estadísticas no paramétricas e impulsado por el auge de la computación en el siglo XX. Este método fue introducido por Bradley Efron en 1979. Efron, un profesor de la Universidad de Stanford desarrolló esta técnica como una solución innovadora para estimar la precisión de los estimadores estadísticos cuando se dispone de muestras pequeñas o cuando no se conoce la distribución de probabilidad teórica de los datos. Antes de la invención del Bootstrap, los métodos tradicionales (paramétricos) para la estimación de la varianza de un estadístico dependían de suposiciones fuertes sobre la distribución de los datos, como por ejemplo suponer  normalidad. Sin embargo, en muchos casos prácticos, estos supuestos no se cumplían. Esto hace que los métodos paramétricos resulten inadecuados o poco precisos.  Otra técnica empleada es el método de Jackknife, desarrollado en la década de 1950 por Maurice Quenouille y popularizado más tarde por John Tukey. El método Jackknife es una técnica que implica eliminar una observación de la muestra en cada iteración y recalcular el estadístico de interés. Sin embargo, este método tiene limitaciones cuando se trata de muestras pequeñas o cuando los datos no siguen una distribución normal.

Los supuestos de los métodos estadísticos paramétricos resultan fundamentales para construir intervalos de confianza y realizar pruebas de hipótesis. Sin embargo, en muchas situaciones prácticas, estos supuestos son demasiado restrictivas o inadecuadas, esto motivó el desarrollo de métodos más flexibles.

Bradley Efron propuso una solución a este problema. En su artículo pionero de 1979 titulado “Bootstrap Methods: Another Look at the Jackknife” [1], presenta el método Bootstrap como una alternativa innovadora para estimar la varianza de un estadístico sin la necesidad de realizar suposiciones paramétricas rigurosas.

En sus inicios el método Bootstrap fue visto con escepticismo debido a que requiere de trabajo intensivo de cómputo, que es necesario para obtener los estadísticos de cada muestra obtenida. A medida que aumentó el poder de cómputo, principalmente en la década de 1980, el método se hizo más accesible y práctico. El desarrollo de las computadoras personales popularizó el método, los resultados se obtenían de manera más rápida y eficiente.    

A lo largo de la década de  1980 y 1990, el Bootstrap se formalizó y se extendió en muchas direcciones. En 1986, Efron y Tibshirani [2] publicaron un artículo que explica como este método puede ser empleado para realizar pruebas de hipótesis y construir intervalos de confianza. Este artículo sentó las bases teóricas del método y lo legitimó en la comunidad estadística.  En 1993, estos mismos autores publicaron el libro “An introduction to the Bootstrap” [3], que sistematizó y popularizó es uso de la técnica entre una audiencia más amplia. El éxito del Bootstrap inspiró el desarrollo de otras variantes del método. Por ejemplo, el Percentile Bootstrap y el Bias-Corrected Boostrap, que fueron algunas extensiones para mejorar la precisión del método en diferentes contextos. También surgió el Bootstrap para datos dependientes, que se aplica a datos que no son independientes, como es usual en series de tiempo.  

Bootstrap No Paramétrico

La idea central del Bootstrap es el remuestreo con reemplazo. A partir de una sola muestra se generan múltiples muestras de  la muestra, cada una de las cuales es del mismo tamaño y seleccionada de manera aleatoria de la muestra original, con la posibilidad de que un mismo elemento pueda ser seleccionado en más de una sola ocasión. Las técnicas de remuestreo consisten en obtener remuestras a partir de la muestra original. Esto permite evaluar diferentes propiedades de los estimadores. En este sentido la técnica Bootstrap se puede considerar como un plan de remuestreo para facilitar el error del estadístico, ya sea en cuanto al sesgo o el error estándar en una predicción.

La forma en que la técnica de Bootstrap realiza el remuestreo puede resumirse en los siguientes pasos:

Paso 1. Seleccionar el estadístico de interés. El usuario seleccionar un estadístico de interés \(\hat{\theta}\), que bien puede ser la media, mediana, correlación, etc.   

Paso 2. Obtener los datos. Se obtiene una muestra, que llamaremos muestra original, que consiste en la realización de variables aleatorias independientes e idénticamente distribuidas, operativamente puede considerarse como realizaciones de una variable aleatoria. Representamos esta muestra original mediante \(\left\{x_{1},x_{2},\ldots,x_{n}\right\}\).

Paso 3.  Generar las muestras Bootstrap. A partir de la muestra original, obtenida en el paso 2, se generan la remuestras Bootstrap, las cuales denotaremos por \(\left\{x_{1,i}^{*},x_{2,1}^{*},\ldots,x_{n,i}^{*}\right\}\), donde el subíndice \(i=1,2,\ldots,B\), y denota que los datos corresponden a la i-ésima muestra de Bootstrap. Cada remuestra o réplica consiste en una muestra de tamaño obtenida de la muestra original con reemplazo. Es decir, un mismo valor de la muestra original puede ser seleccionado en más de una ocasión,  o bien no ser seleccionado. Por lo general se selecciona al menos \(B=1000\) remuestras, con el objetivo de tener una buena aproximación a la distribución del estadístico de interés \(\hat{\theta}\).

Paso 4. Evaluar el estadístico de interés en cada remuestra. Para cada réplica o remuestra de Bootstrap, obtenida en el paso 3, se calcula el valor del estadístico de interés \(\hat{\theta}\), que para diferenciarlos del calculado sobre los valores de la muestra original,  lo denotaremos por \({\hat{\theta}}^{\ast i}=\hat{\theta}\left(x_{1,i}^\ast,x_{2,i}^\ast,\ldots x_{n,i}^\ast\right)\).

Paso 5.  Estimación de la distribución empírica del estadístico de interés.

Después de calcular el estadístico de interés en cada una de las remuestras de Bootstrap, es factible a partir de los valores \(\left\{{{\hat{\theta}}^{\ast 1}},{{\hat{\theta}}^{\ast 2}},\ldots,{{\hat{\theta}}^{\ast B}}\right\}\) obtener una distribución empírica del estadístico de interés \(\hat{\theta}\). A través de esta distribución se puede evaluar la variabilidad del estadístico sin necesidad de hacer supuestos adicionales sobre la distribución teórica que dio origen a la muestra original. 

Ahora, queda más claro el empleo del nombre Bootstrap, pues la técnica refleja el hecho de que el método utiliza sus propios datos para estimar la variabilidad sin la necesidad de información adicional como lo hacen los métodos paramétricos.     

Estimaciones Bootstrap del error estadístico.

En el paso 5 del método descrito anteriormente contamos con un gran número de estimaciones Bootstrap del estadístico de interés  \(\hat{\theta}\), es decir el conjunto de los valores \(\left\{{{\hat{\theta}}^{\ast 1}},{{\hat{\theta}}^{\ast 2}},\ldots,{{\hat{\theta}}^{\ast B}}\right\}\) a partir del cual obtenemos la estimación Bootstrap de la distribución del estadístico de interés, que usualmente se llama distribución muestral Bootstrap de la distribución muestral de  \(\hat{\theta}\).

De entre los errores estadísticos de mayor importancia en la estadística se encuentra el error estándar o desviación estándar de la distribución muestral de un estadístico. La estimación Bootstrap de la desviación estándar queda definido por la expresión

\({\hat{\theta}}_{BOOT}=\sqrt{\frac{1}{B-1}\sum_{i=1}^{B}\left ( {\hat{\theta}}^{*i}-\bar{{\hat{\theta}}^\ast} \right )^2}\),

donde corresponde a la estimación Bootstrap de la media muestral de la distribución Bootstrap, obtenida a través de la expresión

\(\bar{{\hat{\theta}}^\ast}=\frac{1}{B} \sum_{i=1}^{B}{\hat{\theta}}^{*i}\)

Intervalos de confianza Bootstrap.

Con la distribución muestral Bootstrap de la distribución muestral de \({\theta}\) se pueden también construir intervalos de confianza del parámetro de interés. El método más común es usar los percentiles de la distribución muestral Bootstrap para definir un intervalo de confianza. Por ejemplo, para un intervalo de confianza del 95% se consideran los percentiles 2.5% y 97.5% de la distribución muestral. Alternativamente, cuando se sospecha que la estimación está sesgada, se puede recurrir el Bias-Corrected Boostrap para ajustar el intervalo. 

Bootstrap Paramétrico.

En ocasiones, el investigador conoce la familia de distribuciones de probabilidad \(F\left ( {\theta} \right )\) que dio origen a los datos, excepto por el valor o vector de parámetros \({\theta}\).  En este caso se estima el valor del vector de parámetros a partir de la muestra, por ejemplo por máxima verosimilitud, denotando esta estimación por \(\hat{\theta}\). En este caso el paso 3 del método Bootstrap No paramétrico se modifica de tal manera que las remuestras \(\left\{x_{1,i}^{*},x_{2,1}^{*},\ldots,x_{n,i}^{*}\right\}\) se obtienen a partir de la distribución \(F\left ( \hat{\theta} \right )\).

Ejemplo. Tomado de (Casella & Berge, 2002) [4]. Consideremos una muestra

-1.81, 0.63, 2.22, 2.41, 2.95, 4.16, 4.24, 4.53, 5.09

Y que es de interés analizar el estadístico de la varianza muestra \(S^{2}\). Con base en una colección de \(B=10000\) réplicas Bootstrap podemos estimar la distribución muestral del estadístico , la cual se muestra en la figura siguiente:

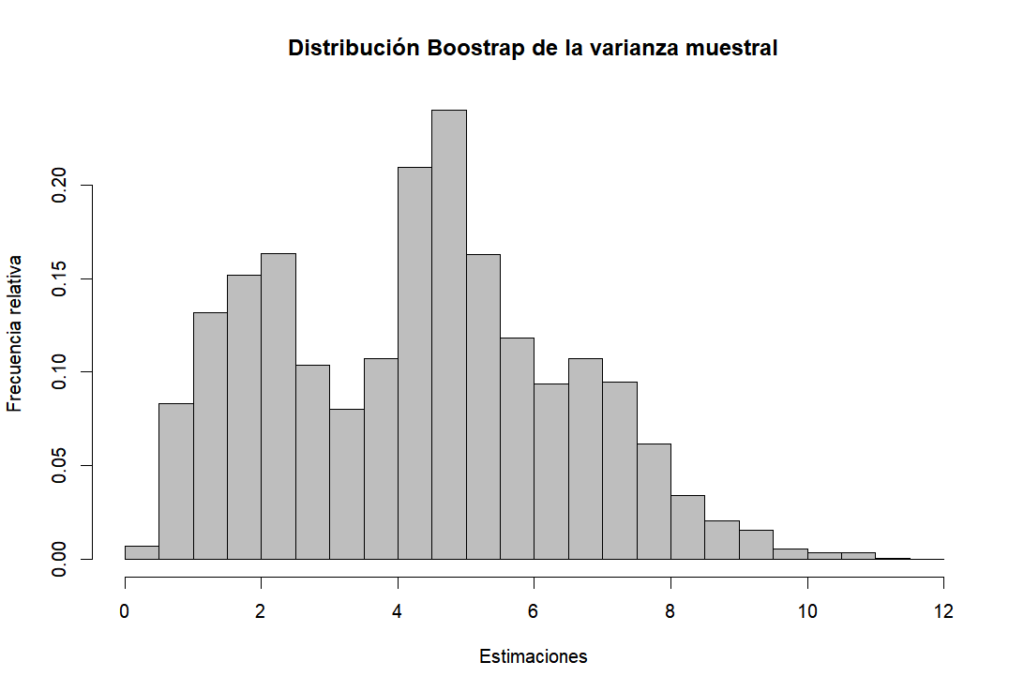
A partir de las estimaciones realizadas en cada réplica obtenemos un valor promedio para \(S^{2}\) de 4.2929 con un error estadístico de 2.1426. Utilizando el método de percentiles, se estima un intervalo del 95% de confianza para \(S^{2}\) dado por (0.860, 8.471).

Si por otro lado, suponemos que la distribución es normal, entonces a partir de los datos se observa que \(\bar{x}=2.7133\) y \(S^{2}=4.8206\). De este modo, el Bootstrap paramétrico tomará muestras de una distribución \(N\left ( 2.7133,4.2848 \right )\). Tomando la misma cantidad de réplicas que antes, obtenemos un valor promedio para \(S^{2}\) de 4.2850 con un error estadístico de 2.1142. Bajo el supuesto de normalidad se sabe que el estadístico \(\frac{\left ( n-1 \right )S^{2}}{\sigma ^{2}}\) tiene una distribución ji-cuadrado con \(n-1\) grados de libertad, por lo que  \(Var\left(S^2\right)=\frac{2\sigma^4}{\left(n-1\right)}\), la cual podemos estimar por máxima verosimilitud para obtener un error estadístico de 2.1424. En este caso,  el método Bootstrap paramétrico realiza una mejor estimación.

Conclusión

Desde su invención, el Bootstrap ha sido aplicado en una gran variedad de disciplinas. En economía se utiliza para calcular intervalos de confianza en modelos econométricos. En biología para analizar datos de muestras pequeñas o con distribución no normal. En metrología, como hemos visto es clave para estimar la incertidumbre de las mediciones. También ha sido ampliamente aplicado e ingeniería para el análisis de fiabilidad. De manera más reciente, el método se aplica para realizar validación cruzada en métodos de aprendizaje automático y ciencia de datos.

La técnica Bootstrap es quizás una de las invenciones más influyentes de  estadística moderna y su impacto ha perdurado gracias a su flexibilidad y aplicabilidad en una diversidad de problemas. A partir de una muestra pequeña de datos, se pueden realizar inferencias robustas sin depender de suposiciones paramétricas fuertes. Esto ha convertido el método en una herramienta esencial en metrología y más allá. Su simplicidad conceptual y el poder actual de cómputo consolida al Bootstrap en la historia de la estadística como una técnica revolucionara del siglo XX.

Referencias

[1] Efron, B. (1979). Bootstrap methods: Another look at the jackknife. The Annals of Statistics, 7(1), 1-26. https://doi.org/10.1214/aos/1176344552.

[2] Efron, B., & Tibshirani, R. (1986). Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statistical Science, 1(1), 54-75. https://doi.org/10.1214/ss/1177013815

[3] Efron, B., & Tibshirani, R. J. (1993). An introduction to the bootstrap. Chapman & Hall/CRC.

[4] Casella, G., & Berger, R. L. (2002). Statistical inference (2nd ed.). Duxbury