Eusebio Bernabeu (1), Tomás Belenguer (2), María Nieves Medina (3)
(1) Instituto Universitario de Ciencias Ambientales- IUCA- Universidad Complutense de Madrid, España.
(2) Departamento de Óptica. Facultad de Óptica y Optometría. Universidad Complutense de Madrid. Laboratorio de Investigación Espacial – LINES- Instituto Nacional de Técnica Aeroespacial- INTA- Torrejón de Ardoz, España.
(3) Área de Masas y Magnitudes Mecánicas. Centro Español de Metrología. Tres Cantos, España.



Resumen
El “Pascal Cuántico” es un proyecto de desarrollo tecnológico límite que permitirá establecer una trazabilidad entre las medidas de presión y las de los patrones primarios de longitud y frecuencia a partir de las determinaciones muy precisas del índice de refracción en gases nobles, preferentemente He, Ar, Kr y algunas moléculas sencillas N2 y CH4, mediante un interferómetro dual de Fabry-Pérot. Este artículo constituye una aproximación dimensional y de análisis de las alternativas de configuraciones ópticas posibles, tecnológicamente viables, que permitan guiar al CEM a la toma de decisiones sobre la solución constructiva más oportuna para el desarrollo y puesta en operación de un equipamiento de estas características extremas en cuanto a precisión e incertidumbre.
Palabras clave: presión, interferómetro Fabry-Pérot, patrón primario.
Abstract:
The “Quantum Pascal” is an outstanding technological development project that will provide traceability between the pressure measurements and length and frequency primary standards based on very precise determinations of the refractive index in noble gases, preferably He, Ar, Kr and some simple molecules N2 and CH4, by means of a dual Fabry-Pérot interferometer. This article constitutes a dimensional approximation and analysis of the alternatives of possible technologically feasible optical configurations, which will serve as a guidance for CEM on the decision for the best constructive solution for the development and operation of an equipment with these extreme characteristics in terms of accuracy and uncertainty.
Key words: pressure, Fabry-Pérot interferometer, primary standard.
1. INTRODUCCION
La metrología de la magnitud presión se divide en dos campos, la presión propiamente dicha y el vacío. En el campo de presión los patrones son puramente mecánicos y están basados en la definición de presión como fuerza por unidad de superficie: son las balanzas de pesos muertos y las columnas de líquido, que se basan en el famoso experimento de Torricelli. El CEM ya posee una demostrada experiencia en dichos patrones, disponiendo de trazabilidad hasta 109 Pa. En el campo de vacío los patrones primarios están basados en la determinación del número de moléculas de un gas. Esta determinación está basada en la mecánica clásica, más concretamente en las leyes de la termodinámica y la mecánica de fluidos. El CEM también posee una dilatada experiencia en este campo, en donde dispone de patrones hasta 10-6 Pa.
Las nuevas tendencias para proporcionar trazabilidad en la magnitud presión tienen un fundamento muy diferente y novedoso, se basan en la fotónica, que trata sobre la interacción entre luz y materia para determinar las propiedades físicas de esta última.
El gran desafío es el desarrollo de un patrón primario de presión, esto es, un patrón que no tenga referencia a otros patrones de presión. La metrología cuántica basada en la interacción entre luz y materia nos ofrece una posibilidad muy interesante para lograrlo, ya que la velocidad de la luz depende de la densidad del medio en el que viaja, basada en la relación entre el número de moléculas de un gas, el índice de refracción y la temperatura del medio. Dado que en condiciones de vacío el índice de refracción es sobradamente conocido, la idea es determinar la presión a partir de los cambios en el índice de refracción en un camino óptico de longitud conocida, siendo estos determinados por medio de un interferómetro láser. Estos prototipos están obteniendo buenos resultados en presiones cercanas a la atmosférica.
Los antecedentes de recurrir a la medida diferencial por métodos interferométricos del índice de refracción de gases respecto a la del vacío se encuentran en la utilización del interferómetro de doble haz de Jamin [1] para medida del índice de refracción del aire, gases nobles y gases y vapores de especies moleculares sencillas, también el interferómetro de división del frente de onda de Rayleigh [2] que sirvió con ventajas de estabilidad y precisión para ese fin. En ambos interferómetros, la medida diferencial del índice de refracción se establece entre el tránsito de la luz en dos trayectorias de idénticas dimensiones (una a través del gas o vapor y la otra a través del vacío), por lo que la señal observable (registrable) es proporcional a una función coseno más un fondo continuo constante o casi-constante: la relación amplitud/fondo determina el contraste (visibilidad de las franjas de interferencia), dependiente de las condiciones operativas del montaje, y el periodo de la función coseno extraíble de la figura interferencial (anillos para el interferómetro Jamin y franjas paralelas para el interferómetro de Rayleigh) que depende linealmente del índice de refracción. La precisión alcanzable con estos dispositivos ópticos tiene su límite en la sexta cifra significativa [3]. Es probable que con la tecnología de hoy, para estos formatos de interferómetros, se podría mejorar en dos órdenes su precisión (hasta la octava cifra significativa).
Los resultados de medidas del índice de refracción en gases, vapores y mezclas proporcionales entre ellos indujeron, por eso años de la mitad del XIX, el nuevo concepto de refractividad molar (refractividad atómica para sustancias monoatómicas) y propiciaron formulaciones, como la Clausius-Mossotti [4], que encaminaron al estudio de las fuerzas de cohesión molecular y de los procesos de adsorción superficial. Estas formulaciones teóricas de esa época conectaban la teoría fenomenológica de Maxwell con la teoría atomística de la materia al incorporar el concepto de “mol” y utilizar la que ahora se considera como constante de Avogadro [5].
Un salto cuantitativo importante para la precisión metrológica con dispositivos interferométricos se produce con la doble propuesta que Alfred Pérot y Charles Fabry realizaron [6] en 1898 de lo que hoy se conoce como interferómetro de Fabry-Pérot. Este dispositivo basado en interferencias de múltiples haces presenta una intensidad de luz transmitida con periodicidad análoga a la de los interferómetros de doble haz, como el citado de Jamin o el bien conocido de Michelson, pero con una estructura en los máximos mucho más acentuados y estrechos. La respuesta funcional teórica de un interferómetro de Fabry-Pérot es la conocida expresión (1) ya dada inicialmente en [6]:
\(T(n,d,\Theta)=\frac{1}{1+\frac{4R}{(1-R^{2})}\sin ^{2}\frac{\delta(\Theta ) }{2}}\) (1)
da cuenta de la intensidad relativa de luz transmitida ITrespecto de la incidente I0 como factor de transmisión T = IT/I0 , del que explicitamos su dependencia del índice de refracción n, de la distancia d de separación entre los dos espejos plano-paralelos y el ángulo azimutal q, como parámetros determinantes que controlan la respuesta del dispositivo. Un esquema de un dispositivo interferómetrico de Fabry-Pérot se muestra en la Figura 1.
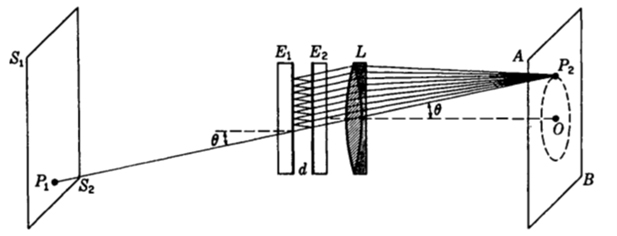
Figura1. Esquema de un interferómetro de Fabry-Pérot: E1 y E2 son los espejos plano-paralelos reflectores, L la lente colectora que lleva a focalizar al plano AB el conjunto de haces de luz emergentes tras las múltiples reflexiones y q es el ángulo azimutal de incidencia.
En la expresión (1) y Figura 1 mostradas R es el factor de reflexión de las caras plano paralelas y δ(θ ) = 2 k n d cosθ , con k = 2π/λ como modulo del vector de onda, en que λ es la longitud de onda central o dominante de la luz incidente considerada monocromática. Esta se deduce considerando la abstracción de onda plana y que toda la configuración geométrica sea perfecta.
A pesar de estas fuertes abstracciones su operatividad como sistema de medida espectral en dispositivos espectrométricos superaba en tres órdenes de magnitud a los de prisma, y en dos órdenes a los de redes de difracción por lo que su incidencia en la nueva física atómica fue determinante: las medidas a nivel de estructura fina (dobletes y multipletes) permitieron asentar los modelos cuánticos atómicos, así como propiciar modelos y teorías sobre las interacciones ente átomos (mayormente alcalinos-gases nobles y moléculas sencillas) [7]. Los progresos tecnológicos en recubrimientos dieléctricos para realizar espejos sin casi pérdidas por absorción (multicapas en láminas delgadas con control de nm, e incluso de 0,1 nm), pulido y control de superficies base en vidrio, cuarzo y materiales cerámicos a niveles de < λ /50, λ /100, junto al progreso en materiales de muy bajo coeficiente de expansión térmica, cerámicas piezoeléctricas y mecánica de precisión van extendiendo los límites metrológicos para los dispositivos Fabry-Pérot al ámbito del análisis espectral de la llamada estructura hiperfina de los sistemas atómicos y moleculares y de las interacciones interatómicos e intermoleculares [7]; es decir, a sensibilidades de detección de la influencia de los núcleos en los espectros atómicos y de los esqueletos nucleares en los moléculares (≈10-13 m).
Sin embargo, el impulso más fuerte por vía de la demanda para el interferómetro de Fabry-Pérot vino del advinimiento de los dispositivos láser. Estos nuevos dispositivos emisores de luz adoptan a este interférometro como cavidad resonante para ondas luminosas a inteccionar con los medios activos capaces de emitir radiación estimulada [8]. Ello amplía la especulación teórica en la ingeniería y el diseño de cavidades Fabry-Pérot [9], pero a esta situación no se hubiera llegado tan ágilmente, si un poco antes no hubiera habido un progesivo análisis de las características reales de los dispositivos interferométricos Fabry-Pérot que va a progresar en paralelo con el desarrollo de la tecnología láser e incidir en la aparición de nuevos formatos. Destaca el interferómetro confocal propuesto por P. Connes [10] que supone un salto en la estabilidad a largo plazo para estos dispositivos interferométricos y en la caracterización funcional de los distintos efectos que propician las condiciones reales: absorción de los medios (espejos) [11], sus defectos ineludibles (pulido y posicionado)[12], la finitud y extensión de las monturas y diafragmas (fundamentalmente el difragma selector) [13]. Ello conduce, finalmente, a asentar fundamentos teóricos nuevos como la teoría difraccional de las cavidades ópticas resonantes de Fox y Lee [14], o el formalismo generalizado de la función instrumental de un Fabry-Pérot como operación de productos de convolución [15] de cada una de estas causas de realidad que se manifiestan asociadas a una función propia definible caracterizable, en muchos casos a priori y, por tanto, que dan origen a una doble ingeniería: de diseño y de tratamiento de resultados. Es en este marco, precisamente, donde podemos estar en condiciones de establecer un diseño intrumental de un Fabry-Pérot que va a operar, además, no con ondas planas sino con luz de un láser monomodo –por lo tanto con haces gaussianos y no con ondas planas ideales- como establece el dispositivo conceptual inicial concebido por C. Fabry y A. Pérot [6].
El propósito de este artículo es dar cuenta de los condicionantes impuestos por un diseño de un interferómetro dual de Fabry-Pérot, con los medios y recursos de la tecnología de hoy, para poder realizar el desarrollo de un dispositivo de prestaciones límites. Prestaciones, tanto por lo que el diseño es capaz de predecir e incorporar con las actuales capacidades, como por la selección de materiales y soluciones técnicas a utilizar; todo ello conducente a un desarrollo constructivo de un dispostivo interferometrico dual Fabry-Pérot de las mejores prestaciones posibles y adecuado a las necesidades requeridas por CEM.
Este artículo se estructura como sigue. En el apartado 2 , siguiente a esta introducción, que presenta los objetivos del Proyecto EMPIR “Quantum Pascal” en el que se encuadra este trabajo, así como los requerimientos impuestos por este proyecto europeo en el que participa CEM. El apartado 3 hace un análisis de distintas alternativas viables a nuestro entender. El apartado 4 es una propuesta inicial para un diseño óptico adecuado que se predimensiona. Finalmente, el apartado 5 es un señalamiento de los posibles puntos críticos a los que el diseño deberá prestar mayor atención, por ser más cruciales o relevantes para el desarrollo del dispositivo interferométrico que se desea construir. Unas conclusiones cierran el trabajo junto con las referencias seleccionadas, en algunos casos, comentadas.
2. PROYECTO “QUANTUM PASCAL”
En línea a lo expuesto el CEM está desarrollando un patrón basado en la determinación de la presión mediante la determinación del índice de refracción. Para realizar este ambicioso proyecto el CEM va a contar con la colaboración de la Universidad Complutense de Madrid y el apoyo del Instituto Nacional de Técnica Aeroespacial, así como con la ayuda de la Universidad Politécnica de Madrid.
Este proyecto persigue conseguir una mejora notable de la trazabilidad actual en presión, migrando la tecnología actual basada en patrones puramente mecánicos, lentos y difíciles de manejar a la cuántica, con un gran potencial tanto de mejora de exactitud y precisión como de manejo. De hecho, la importancia de superar las limitaciones de los patrones de presión actuales ha sido identificada como un objetivo estratégico por el CIPM (Comité Internacional de Pesas y Medidas), por el Comité Consultivo para la Masa y Magnitudes Relacionadas (CCM) y el Comité Técnico de EURAMET para la Masa y Magnitudes Relacionadas (TC-M).
Además, el CEM está participando con financiación en el proyecto europeo EMPIR 18SIB04 QuantumPascal “Towards quantum-based realisations of the pascal” (Hacia las realizaciones cuánticas del pascal) [16]. El objetivo general del proyecto es desarrollar nuevos patrones de presión cuánticos basados en métodos ópticos, de microondas y dieléctricos y evaluar su potencial con el objetivo de reemplazar los patrones de presión existentes basados en la física clásica. El CEM va a participar para mejorar la precisión y ampliar el rango de trabajo de los métodos basados en la refractometría de Fabry Pérot que tienen el potencial de convertirse en patrones primarios de la unidad de presión SI, el pascal. Las incertidumbres objetivo (k = 1) y los rangos de presión son 5×10-4 en el rango 1 Pa – 1 kPa y 1×10-5 en el rango 1 kPa a 100 kPa. Esta participación constituirá una gran oportunidad para el CEM no sólo desde el punto de vista económico, sino porque también permitirá el intercambio de información y experiencia con otros institutos que ya están desarrollando patrones similares como el “Physikalisch-Technische Bundesanstalt” de Alemania, el “Conservatoire National des Arts et Métiers” de Francia, la Universidad de Umea de Suecia o el “Istituto Nazionale di Ricerca Metrologica” de Italia.
Como el rango completo a cubrir en presiones de va de 1 Pa a 100 kPa, conviene para la conformación inicial del interferómetro Fabry-Pérot dual, conocer los valores máximos de índice de refracción de aquellos gases susceptibles de ser objeto de medida por dicho dispositivo.
Una búsqueda bibliográfica bastante exhaustiva nos lleva a recoger los resultados obtenidos por Y. P. Kathuria [17], quizá, los que aparece con más dígitos conseguidos hasta el momento (resolución de 108) para la longitud de onda de interés de CEM (632,8 nm) y con un interferómetro de láser (Hewlett Packard HP5528) en un formato modificado del interferómetro de Michelson básico de este dispositivo comercial. La Tabla 1 recoge reordenada los valores obtenidos para dos gases nobles (He, Ar) y dos moléculas sencillas con propiedades intermoleculares muy próximas. La Tabla 1 incorpora también valores para otro gas noble (Kr) seleccionado por nosotros y considerado de interés [18]. Excluimos, a priori Ne y Xe por su comportamiento intermolecular diferente y más complejo; aunque el He ha sido incluido no está exento de problemática conceptual y del carácter experimental que lo singulariza. Se recoge, no obstante, el valor para el aire seco como posicional experimental accesible (se ha recogido el valor de menor humedad; es decir, más seco de los dados por [17]).
Tabla 1. Índices de refracción medidos de varios gases nobles (He, Ar, Kr) y dos moléculas sencillas (N2 y CH4). También se incluye el aire seco (» 12 Pa de presión parcial del vapor de agua residual para caracterizar humedad). Las medidas se refieren a presión en todos los casos de ≈ 100 kPa
| Gas (pureza /%) | Índice de Refracción | Temperatura (K) | Referencia |
| He (99,99) | 1,000 0319 8 | 301,96 | [17] |
| Ar (99,9) | 1,000 256 59 | 302,16 | [17] |
| Kr ( 99,7) | 1,000 428 47 | 288,16 | [18] |
| N2 (99,9) | 1,000 267 36 | 302,16 | [17] |
| CH4 (99,3) | 1,000 418 07 | 301,66 | [17] |
| Aire seco | 1,000 260 7(41) | 297,36 | [17] |
3. DIMENSIONADO PRELIMINAR PARA UN INTERFEROMETRO BASICO FABRY-PÉROT
Al objeto de aproximar órdenes de magnitud y establecer un dimensionado preliminar que permita ajustarse los requerimientos del Proyecto Quantum Pascal mostramos en las Tablas 2 y 3 un conjunto de variables características de un interferómetro básico de Fabry-Pérot; es decir, aquel que responde de una manera “ideal” –abstracta- a la ecuación dada (1). Se trata pues de interferométro de Fabry-Pérot plano, perfectamente ajustado en paralelismo, obviadas consideración de limitaciones ópticas (ópticas colimadora y colectora perfectas, tolerancias de pulido en los espejos y de las multicapas dieléctricas reflectoras no consideradas, absorbancias de los materiales despreciables, tamaño del diafragma selector puntual, entre otras…) y, además, considerando la luz estrictamente monocromática y con comportamiento ideal de onda plana de frente de onda infinito. Como longitud de onda para la luz de trabajo hemos tomado 633 nm, accesible con un láser diodo estabilizado en corriente y temperatura que pueda tener trazabilidad con el Peine de Frecuencias del CEM (19).
De los valores de índices de refracción de la Tabla 1 tomamos aquellos de mayor y menor valor (Kr y He) para analizar a distintos valores de la separación entre espejos –d– el número de orden interferencial y el número de ordenes detectables en un rango completo de medida del índice de refracción desde en vacío (n = 1) al de gas (He o Kr) a presión de 100 kPa, así como el número de órdenes interferenciales que se presentarán en ambos casos considerados de gases nobles susceptibles de ser medidos. Ello es importante pues determina, en cada caso, el número de puntos experimentales singulares de medida en el rango dinámico completo del dispositivo.
Tabla2. Orden interferencial K0 de trabajo en un F-P básico en función de la separación d entre espejos plano-paralelos, así como en número de órdenes interferenciales ΔK0 que se presentarán como puntos singulares de medida en el rango dinámico de presión de 0kPa a 100 kPa para He, Ar y Kr.
| He | Ar | Kr | Observaciones | ||
| d (mm) | K0 | ΔK0 | ΔK0 | ΔK0 | |
| 40 | 126,383 | 4 | 33 | 54 | excluido |
| 60 | 189,573 | 6 | 49 | 80 | |
| 80 | 252,765 | 8 | 65 | 108 |
Se ha considerado conveniente incluir al Ar como un gas muy operativo y manipulable en laboratorio.
El orden interferencial K0 se determina para eje del sistema óptico (θ = 0) por 2d = K0 λ y ΔK0 por la expresión 2(n -1) d = ΔK0λ, siendo n el índice de refracción n del gas considerado a presión de 100 kPa.
Los resultados ya evidencian que la separación entre espejos de 40 mm debe considerarse excluible, dado que 4 puntos singulares de medida para el caso del He parecen pocos para establecer un conjunto estadístico del que inferir resultados posteriores por tratamiento de esos datos. Mantenemos los valores de d = 60 mm y 80 mm como de posible consideración.
La Tabla 3 permite comparar, para estas dos distancias – d – ya consideradas, unas magnitudes determinantes en los procesos de medida con un F-P: el intervalo espectral libre, Δυ, y el elemento espectral de referencia, δυ, que expresamos ambos en frecuencia para obviar la dependencia del índice de refracción. El intervalo espectral libre representa la capacidad dinámica de recorrido entre órdenes interferenciales consecutivos y determina la condición necesaria para evitación de injerencia -superposición entre órdenes interferenciales- y, por lo tanto, fija la extensión de la escala medible. El elemento espectral de referencia es el paso de cuenta o unidad básica de la incertidumbre en la medida. También se le asocia, en lenguaje de algebra convolutiva, como anchura de la función instrumental considerada ésta como una generalización de su concepto al incorporar todas las causas instrumentales que determinan la incertidumbre de la magnitud medible.
Las relaciones que permiten establecer estos valores son: F= 4R/(1-R)2, conocido como fineza reflectiva e identificable en la ecuación (1), ℱ = π√F/2 es la fineza operativa, entendida como el número de haces de luz que intervienen eficazmente en la conformación de la señal interferencial, el intervalo espectral libre Δυ= 2c/λℱ, y elemento espectral de referencia δυ=ℱ K0 =c/4 d ℱ.
Tabla 3.- Intervalo espectral libre Δυ y elemento espectral de referencia Δυ
| d (mm) | R (%) | F | ℱ | Δυ(GHz) | δυ(MHz) |
| 60 | 96 | 2,400 | 77 | 2,50 | 16,20 |
| 60 | 97 | 4,311 | 103 | 1,87 | 12,14 |
| 80 | 96 | 2,400 | 77 | 2,50 | 12,17 |
| 80 | 97 | 4,311 | 103 | 1,87 | 9,10 |
| 60 | 98 | 9,800 | 155 | 2,50 | 8,05 |
| 80 | 98 | 9,800 | 155 | 1,87 | 6,05 |
En todos los casos considerados el intervalo espectral libre es suficiente, pues rebasa en más de dos órdenes al elemento espectral de referencia, aún extendida éste elemento espectral a la anchura de la función instrumental, lo que difícilmente supondría un incremento de su valor en factor x10. Los valores recogidos en las dos últimas filas y sombreados, serán considerados más adelante y, en principio, una reflectividad tan elevada plantea problemas en el contraste de la señal detectable por pérdida de la irradiancia a nivel de detector, excepto que una inyección del haz de luz por fibra óptica paliara esta dificultad al utilizar un espejo con reflectividad al 97 % y el otro (por el que se inyecta la luz con la fibra óptica) al 100 %. Ello permitiría alcanzar una refectividad equivalente al 98 %, con un contraste razonable, análogo a los de los otros casos considerados en las cuatro primeras filas de la Tabla 3.
4. ALTERNATIVAS PARA UN DISEÑO ÓPTICO
Sin embargo, hoy se conocen alternativas potentes con prestaciones singulares a la del interferómetro básico inicial de Fabry-Pérot. Estas alternativas de distintas configuraciones permiten, en muchos casos, preservar la estructura del intervalo espectral libre que se elige para conseguir mejorías en la fineza operativa ℱ y, sobretodo, alcanzar un régimen de estabilidad a largo plazo, lo que es muy determinante a la hora de optar por la solución experimental a escoger.
Por ello, para configurar una propuesta de diseño, se ha considerado recurrir a la configuración de resonador estable [8, 9] que, como es sabido, se relaciona con la expresión: 0≤ g1⋅g2 ≤1, siendo gi (i=1, 2) y, \(g_{i}=1-\frac{d}{r_{i}}\) en la que d representa la distancia entre espejos 1 y 2 del interferómetro F-P y ri el radio de curvatura de cada uno de los dos espejos que lo constituyen.
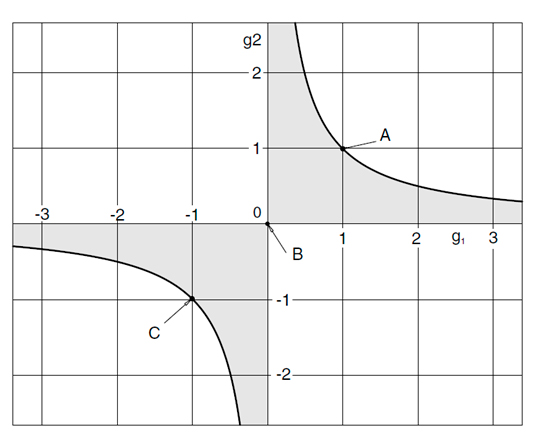
Las configuraciones estables, es decir aquellas que confinan un modo con órdenes interferenciales resonantes, se recogen en la zona sombreada gris de la Figura 2. La configuración con mayor fineza se consigue en una configuración resonador confocal (punto B de la Figura 2), en la que r1=r2=r=d y g1 y g2 son, por lo tanto, nulos. Esta configuración es la más estable frente a desalineamientos y, por lo tanto, prioritaria para una elección adecuada. Otro caso considerado es el denominado FP de espejos planos (la considera como básica) en los que g1=g2 son nulos dado que son entonces de radio de curvatura infinita (Punto A en la figura 1). Esta configuración presenta problemas de estabilidad al desalineamiento de los espejos constituyentes, principalmente en montajes sellados que se requieran a largo plazo. Existe también la denominada configuración concéntrica, en la que d=2r siendo, en este caso, los radios de curvatura de cada espejo iguales entre sí por lo g1=g2=-1 (punto C en la Figura 2).
En el diseño de un interferómetro Fabry-Pérot confocal es necesario considerar que el haz de salida de la fuente láser debe ser colimada por una óptica adicional que inyectará este haz sobre un sistema óptico especial que permitirá que los haces de interés sean introducidos en la cavidad láser apropiadamente. Hay que tener en cuenta que el espejo de la cavidad se comporta como un singlete divergente que desenfoca el haz incidente en la cavidad. Para evitar esto, debe incluirse un singlete convergente que permita expandir el haz apropiadamente y confinar el modo como en un sistema confocal propiamente dicho. Esta combinación de elementos se recoge en la siguiente figura (Figura 3), en la que se incluye al dispositivo óptico trabajando en modo de inyección del haz de entrada y de extracción del haz de salida. En el diseño planteado todos los elementos son de material sílice fundida (también podría considerarse en Zerodur) y el sistema así constituido es estrictamente simétrico.
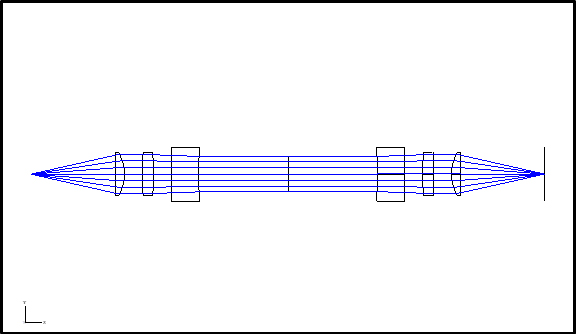
Un interferómetro F-P confocal tiene, por configuración óptica de recorrido, justo el doble de un F-P plano para la misma envergadura instrumental por lo que, a igual tamaño, se tendría doble de órdenes interferenciales ΔK0, lo que resultaría muy beneficioso al doblar el número de puntos singulares registrables en un barrido de presión de vacío a 100 kPa. Ello es especialmente relevante para el caso de gas He. El elemento espectral de referencia debiera verse minorado en un factor 2 equivalente, pero ello no es tan optimista porque los espejos esféricos presentan una aberración esférica que determinan una fineza geométrica Fg = r3λ/4ρ4 que habría que controlar considerando que r es el radio de curvatura impuesto por el formato adoptado y r el diámetro del haz operativo del interferómetro, diámetro que sí es controlable. Finalmente, queremos lanzar una atractiva y novedosa posibilidad tecnológica: sustituir la óptica de inyección en el F-P confocal por una entrada directa de una fibra óptica monomodo que preserve la polarización y de diámetro muy reducido, a la que habría de conseguir acoplar sin cubierta protectora (tan sólo su núcleo y “clading”) a uno de los espejos confocales en eje. Este espejo con reflectividad al 100 %, elevaría al sistema a una reflectividad media geométrica equivalente a 98 %, que como se muestra en las filas sombreadas de la Tabla 3 obtiene unos valores muy satisfactorios, pero –en esta circunstancia- sí disminuir la tasa de contraste. Dos hechos deben de acontecer para otorgar prioridad a esta opción: que los efectos de la inserción de la fibra óptica en el espejo confocal de reflectividad no promuevan efectos difractivos que degraden la señal de salida, el otro más posiblemente accesible estriba en que la propia dinámica de las reflexiones múltiples establezca un rápido y progresivo régimen que restaure el modo principal dominante en el dispositivo resonante. Aunque, en parte, ambos requisitos son interdependientes, la verificación a escala de simulación y, sobretodo, la propia validación experimental directa pueden concluir sobre su viabilidad.
4. HERRAMIENTAS PARA EL ANALISIS DEL DISEÑO OPTICO DEL INTERFERÓMETRO DE
FABRY-PÉROT
Para verificar el comportamiento de las distintas configuraciones y opciones posibles a considerar para el interferómetro Fabry-Pérot se pretende realizar un análisis comparativo entre todas estas posibilidades en busca de la mejor solución viable. Para ello contamos con la potente herramienta de cálculo automático no-secuencial ASAP [20].
A título de ejemplo, mostramos en lo que sigue cómo un haz divergente, que simula la salida de un haz de luz de una fibra óptica, es inyectado debidamente en la cavidad confocal F-P. El haz focalizado en el interior de los espejos confina la luz, lo que pone de manifiesto la naturaleza confocal de la configuración propuesta.
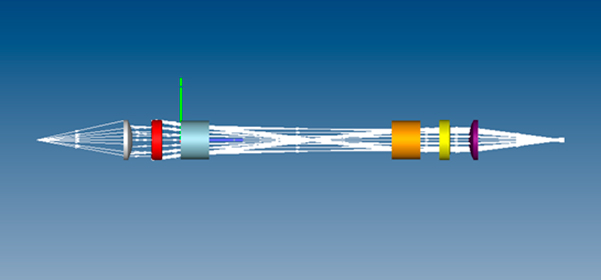
Según este esquema de trabajo, la señal es extraída por un conjunto óptico expansor, situado a la derecha del dispositivo confocal, donde con un sistema óptico singlete idéntico al de la fase de inyección, la señal luminosa es recogida por una fibra óptica en conjunción de sus aperturas angulares para que el propio diámetro de la fibra óptica actúe de diafragma selector. La fibra óptica conduce la señal al detector, generalmente un fotodiodo de gran superficie que asegure buena responsividad o, eventualmente ante señales muy bajas, un fotodiodo de avalancha en conexión por acoplo directo con la fibra óptica.
Las Figuras 5 y 6 muestran el funcionamiento de la cavidad confocal inyectando luz láser monomodo de modo TEM00 con la estructura perfilométrica XY, tal como se muestra en la Figura 5, tomada como señal de entrada.
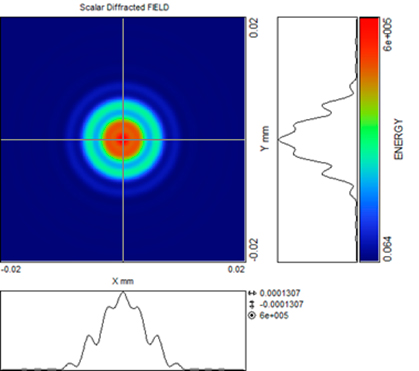
La simulación de la respuesta espectral del resonador al variar 2 nm la radiación incidente en el dispositivo, pero manteniendo fija la geometría inicial, pone de manifiesto la alta sensibilidad del dispositivo como se aprecia en la siguiente Figura 6 –señal de salida.
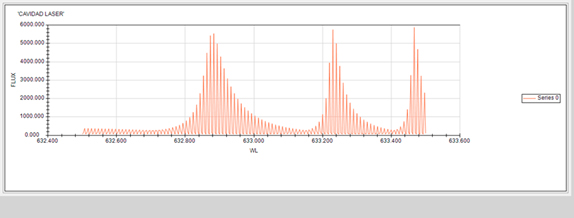
Este resultado ha sido obtenido con el propósito de ver la transferencia de modos resonantes a d y n fijos. Circunstancias que no se corresponden con la funcionalidad prevista para el F-P confocal dual por variación de presión del gas en uno de sus canales, pero que informan de cómo un sistema confocal con inyección y extracción simétrica se comporta. La Figura 6 informa sobre buena calidad de señal en la zona de los máximos principales, también pone de manifiesto una esperable disimetría de los modos transferidos. Disimetría que su envolvente recuerda al bien conocido perfil de Fano [22], evidencia clara de existencia de procesos disipativos. No cabe pensar que estén ligados a procesos de absorción, como se han estudiado para un F-P abundantemente [23], dado que ASAP incorpora variables únicamente de óptica geométrica, sino más bien estén ligados a la incidencia de la aberración esférica. Su control debe ser objeto de una singular atención.
6. OTRAS CONSIDERACIONES Y CONCLUSIONES PROVISIONALES
Este artículo pone de manifiesto las dimensiones físicas y de envergadura aconsejables para un interferómetro Fabry-Pérot dual, a ser posible sellado por contacto óptico de sus espejos, como forma de obviar sistemas de alineamiento móvil. Este requisito impone el recurso obligado de un interferómetro F-P confocal. No obstante, un equipamiento de estas prestaciones no sólo viene impuesto por el dispositivo óptico que lo soporta sino por toda la cadena instrumental y proceso de datos que lo soporta. A este respecto conviene señalar, que la fuente de luz, un diodo láser estabilizado en temperatura y corriente, puede no ser la mejor opción deseable. Láseres de He-Ne estabilizados con dos modos competitivos desdoblados por efecto Zeeman [24] han sido utilizados en metrología dimensional y con trazabilidad con el peine de frecuencias de CEM [19]. Esta cualidad de utilizar un espectro dual abre la posibilidad de establecer una metodología en el tratamiento de datos donde la variable a extraer no sea la medida del índice de refracción de un gas o conjunto de gases seleccionados, sino de la dispersión espectral en el intervalo fijo, estable y trazable de la diferencia de los dos modos espectrales desdoblados de un láser de He-Ne. La ley funcional de la dispersión espectral para gases nobles y moléculas sencillas está bien establecida – ley de Cauchy- y probablemente los algoritmos que la conecten con la refractividad molar o atómica es de las especies medibles sea más directa.
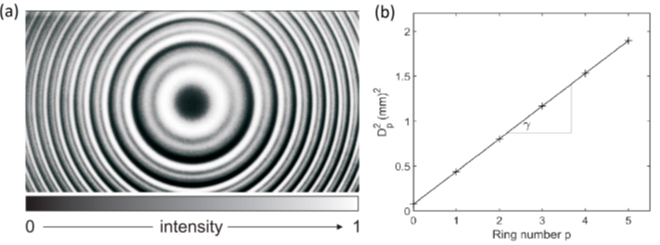
También merece especial atención operar en exclusividad con el modo principal en eje seleccionado por un diafragma selector, sino operar en campo abierto contando con la formación de anillos en un interferómetro de Fabry-Pérot, en configuración confocal incluida. Véase la dependencia del ángulo de incidencia θ de la intensidad transmitida por un interferómetro de F-P en la ecuación (1) y en Figura 7, figura precisamente elegida por corresponder a dos longitudes de onda en la fuente de luz utilizada. Hoy existen excelentes cámaras CMOS con resolución espacial de 2 µm a 4 µm con prestaciones en tiempo de respuesta ≅µs que facilitan y amplían el campo de toma de datos a toda una imagen con estructura conocida, lo que facilita enormemente el recurso a técnicas estadísticas de tratamiento de datos por ”centroides” y/o por ajustes a datos estructurados. Posiblemente al ser una opción externa al sistema central del interferómetro F-P dual, ellos puede ser objeto de consideración opcional e, inclusive, compartido en un doble uso como elemento sinérgico de control y extracción simultánea de resultados por vía espacial (anillos- cámaras CMOS) y monocanal (anillo central por diafragma selector).
En todo caso, resulta conveniente diferenciar las tareas constructivas de un equipamiento de estas prestaciones y las labores de servicio de extracción y tratamiento de datos y su posterior uso de algoritmos para su conexión con la refractividad molar o atómica, pero tampoco debe obviarse su interdependencia, pues muchas veces viene a medirse no lo más adecuado, sino lo que parece más inmediato o directo. La búsqueda de otros caminos puede conducir a metodologías más directas y con menor propagación de errores. Muy posiblemente este proyecto “Pascal cuántico” responda a un escenario de esta naturaleza.
Referencias
[1] J. Jamin, C.R. Acad. Sci. Paris, (1856) 42, 482
[2] Lord Rayleigh, Proc. Roy. Soc., (1896), 59, 198.
Este interferómetro es una extensión del experimento de la doble rendija de T. Young adecuándolo a una configuración que contuviera dos cubetas (gas y vacío) después de cada rendija.
[3] American Institute of Physics Handbook, (1957) McGraw-Hill, New York, 6– 21.
Transpone valores de índice de refracción de gases y vapores de la Tabla 554 de “Smithsonian Physical Tables”, 1954. También recoge la fórmula empírica de J.B. Biot- F. Arago que expresa la dependencia del índice de refracción de un gas con la presión y la temperatura: \(n_{t}-1=\left ( n_{0}-1 \right )\frac{p}{760}\left ( 1+a\cdot t \right )\) donde a es el coeficiente de expansión térmico del gas, t en °C, p en mmHg y n0 el índice de refracción a 0 °C.
[4] R. Clausius, Mechanische Wärmetheorie, 2 (Braunscheweig, 2nd ed. 1879), p.62
O. F. Mossotti, Mem. Soc. Sci. Modena, (1850) 14, 49.
[5] En el Sistema Internacional de unidades revisado (20.05.2019): mol es la unidad de cantidad de sustancia. Un mol contiene exactamente 6,02214076 × 10 23 entidades elementales (átomos o moléculas). Cifra que se toma como valor numérico fijo y que se corresponde con el denominado NA número de Avogadro expresado en la unidad mol-1.
[6] C. Fabry, A. Pérot, Theorie et applications d’une nouvelle methode de spectroscopie interferentielle, Ann. Chim. Phys., (1899) 16, 7.
A. Pérot, C. Fabry, On the Application of Interference Phenomena to the Solution of Various Problems of Spectroscopy and Metrology, Astrophysical Journal. (1899) 9, 87.
[7] E. Bernabeu, P. Tougne, M. Arditi, Cellules à vapeur de Cesium utilisèes comme filtres hiperfines. C.R. Acad. Sc. Paris, (1969) 268, 321-324.
E. Bernabeu, F. García-Peralta, J.M. Alvarez, Pressure effects of Helium, Neon and Argon on the Hyperfine Structure of the first doublet of Cesium, J. Opt. Soc. Amer. (1977) 67, 24-27.
E. Bernabeu, J.M. Alvarez, Shift and broadening of hyperfine components of the first doublet of Cesium perturbed by foreign gases, Phys. Rev. A (1980) 20, 2690-2695.
[8] A. E. Sigman, Lasers, University Science(1986).
[9] O. Svelto, Principles of Lasers, Springer-Verlag, 4ª ed. (2004).
[10] P. Connes, Rev. D´Opt. (1956) 35, 37; Journ. Phys. (1958) 18, 262
[11] P. Giacomo, Les couches réflechissantes multidielectriques appliquées à l´interferometry de Fabry-Pérot, Rev. D´Opt. (1956) 35, 317-354; 442-467.
12] C. Dufour, R. Picca, Rev. d´Opt. (1945) 24, 19
R. Chabbal, J. Rech. Cent. Nat. Rech. Sci., Labs. Bellevue (París) (1958) 24, 138
[13] P. Jacquinot, J. Opt. Soc. Amer. (1954) 44, 761
[14] A. G. Fox, T. Li, Resonant Modes in a Maser Interferometer, Bell. Tech. J. (1961) 40, 453
H. Kogelnik, T. Li, Laser Beams and Resonators, Proceedings of the IEEE (1966) 54, 1312 -1329. Appl. Opt. (1966) 5, 1550-1567. Publicados ambos a la vez –simultáneamente- y bajo el mismo título.
[15] P. Jacquinot, (1973) Instrumental Interferometry. Atomic, Molecular and Lasers 3 rd. Course. ITPC, Trieste.
[16] https://www.ptb.de/empir2019/quantumpascal/home/
[17] Y.P. Kathuria, Accurate measurement of refractive index of gases using a laser interferometer, J. Optics (Paris) (1991)22, 149-151.
[18] J. Koch. Kungl. Fysiografiska Sällskapets i Lund Förhandlingar (Proceedings of the Royal Physiographic Society at Lund) (1949)19, 173.
(Citado en P. J. Leonard. Refractive indices, Verdet constants, and polarizabilities of the inert gases, Atomic Data and Nuclear Data Tables 14, 21-37 (1974).https://refractiveindex.info/?shelf=main&book=Kr&page=Koch
[19] S.Ferreira-Barragáns, Mª Mar Pérez-Hernández; B. Samoudi, E. Prieto “Realisation of the metre by optical frequency comb: Applications in length metrology’’ SPIE. International Conference on Applications of Optics and Photonics Editor(s): Manuel F. Costa. ISBN: 9780819485755. 8001,80014I-8.
[20] ASAP: Advances System Analysis Program es un software comercial para ingeniería óptica que opera por trazado de rayos, con ventaja sobre otros programas éste da información sobre la luz difusa y puede operar también con haces gaussianos.
[21] R. Kingslake, R.B. Johnson, Lens Desing Fundamentals, 2nd Ed. (2009) Acad. Press & SPIE Eds.
R.G. Gonzalez-Acuña, H.A. Chaparro-Romo, General formula for bi-aspheric singlet lens design free of spherical aberration, Appl. Opt. (2018) 57, 9341-9345.
[22] U. Fano, Effects of configuration interaction on intensities and phase shifts. Phys. Rev. (1961)124, 1866-1872.
[23] J.J. Monzón, L.L. Sánchez-Soto, On the concept of absortion for a Fabry-Perot interferometer Am. J. Phys. (1996) 64, 156-163.
J.J. Monzón, L.L. Sánchez-Soto, E. Bernabeu Influence of coating thickness on the performance of a Fabry-Pérot Interferometer, Appl. Opt. (1991) 30, 4126-32.
J. Xue, et al., Pulsed laser linewidth measurements using Fabry-Pérot interferometer,Results in Phys. (2016) 6, 698-703.
[24] He-Ne laser 2.5 mW. Class 3B. Doublet emission line » 632.8 nm. HP/Agilent.US.









Comentarios