La definición del amperio en el SI revisado

Yolanda A. Sanmamed
Javier Díaz de Aguilar
Centro Español de Metrología
Tres Cantos (Madrid)
yalvarezs@cem.es

Resumen:

Este artículo describe los cambios recientemente realizados en el Sistema Internacional de Unidades (SI), centrándose en lo relativo a la unidad de intensidad de corriente eléctrica, el amperio, y subrayando la importancia que tuvo la entrada en vigor el 20 de mayo de 2019 de la revisión del SI para la metrología eléctrica. Se resumen las principales dificultades de realización de la anterior definición del amperio, y cómo la disponibilidad de patrones cuánticos llevó a la utilización de patrones eléctricos fuera del SI, hasta su actual revisión. Se introduce además la nueva definición del amperio en el SI revisado y las realizaciones prácticas (“mise-en-pratique”) propuestas, resaltando cómo en el SI revisado las constantes de Josephson y von Klitzing, K_J y R_K, tienen valores exactos, una vez fijados los valores numéricos de la constantes de Planck h y la carga elemental e, y cómo las realizaciones de las unidades eléctricas derivadas, voltio y ohmio, obtenidas con los efectos Josephson y Hall cuántico, respectivamente, quedan ya integradas dentro del SI.

Palabras clave: Sistema Internacional, redefinición, amperio, patrón cuántico

Abstract:

This article describes the changes in the International System of Units (SI), focused on the SI unit of electric current, the ampere, highlighting the importance for the electrical metrology of the SI revision with effect from May 20^th 2019. The main drawbacks of the previous ampere definition are summarized together with the previous practical realization in the conventional system of units. The ampere definition in the revised SI and the proposed practical realizations (“mise-en-pratique”) are introduced, underlining that Josephson and Hall constants, K_J and R_K, respectively, have now exact values defined in terms of the fixed numerical values of the Planck constant and elementary charge, h and e. The derived electrical units volt and ohm, obtained with the Josephson and quantum Hall effects, respectively, are now fully integrated within the SI.

Keywords: International System, redefinition, ampere, quantum standard

1.- Introducción

El Sistema Internacional de Unidades (SI) no es estático sino que evoluciona para adaptarse a los requisitos de medición mundiales, cada vez más exigentes. En la vigesimosexta reunión de la Conferencia General de Pesas y Medidas (CGPM), el 16 de noviembre de 2018, se aprobó la redefinición de cuatro unidades básicas del SI: el kilogramo, el amperio, el kelvin y el mol, basándolas en la asignación de  valores numéricos exactos a cuatro constantes universales (figura 1). Esta redefinición entró en vigor el 20 de mayo de 2019, día mundial de la Metrología.

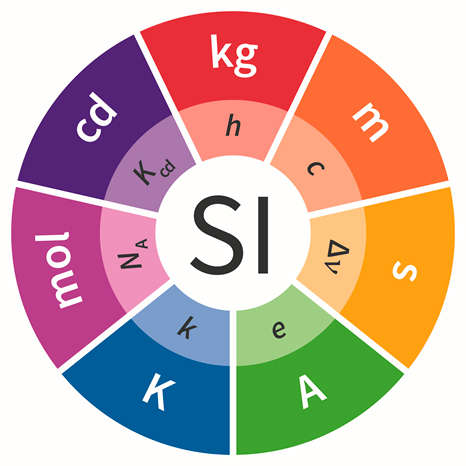
El resultado de la revisión del SI es una definición más coherente y fundamental de todo el SI, prescindiendo de realizaciones prácticas basadas en patrones materiales, pasando a realizaciones prácticas más exactas, además de reproducibles en cualquier tiempo y lugar. El uso de constantes de la naturaleza para definir las unidades de medida internacionales permitirá a la comunidad científica y a la industria obtener y diseminar con mayor exactitud sus mediciones, desde los rangos más pequeños hasta los más grandes, cumpliendo así con los requisitos de medición modernos. En este nuevo SI revisado determinadas constantes universales tendrán valores exactos, sin incertidumbre alguna.

2.- Definición del amperio previo a la redefinición del SI

La definición de amperio en el anterior sistema internacional se adoptó en la novena Conferencia General de Pesas y Medidas en 1948, estableciéndose el amperio como la unidad de intensidad de corriente eléctrica y una de las unidades básicas de dicho sistema, de acuerdo con la siguiente definición:

El amperio es la intensidad de una corriente constante que, manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno del otro, en el vacío, produciría entre esos conductores una fuerza igual a 2×10^-7 newton por metro de longitud.

La fuerza por unidad de longitud resultante de aplicar la ley de Ampere es directamente proporcional al cuadrado de la corriente I e inversamente proporcional a la distancia entre hilos r, tomando para la configuración descrita en la definición del amperio y mostrada en la figura 2 el siguiente valor:

\(\frac{F}{l}=\mu_{0} \frac{l^{2}}{2\pi r}=2 \cdot 10^{-7}N/m\)     (1)

A partir de esta definición se fijaba la permeabilidad magnética del vacío, μ₀, que tenía un valor exacto en el anterior SI, µ₀ = 4π×10^-7 H/m = 4π×10^-7 m^.kg^.s^2.A^-2 y, por lo tanto, el amperio estaba relacionado con las otras unidades básicas: metro, kilogramo y segundo, a través de esta constante. En el anterior SI las unidades eléctricas dependían de las unidades mecánicas.

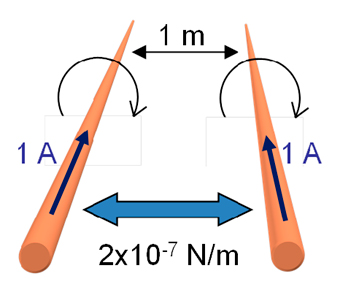
La realización práctica del amperio de acuerdo a su definición en el anterior SI, se realizaba a través del experimento de la balanza de corriente [3], complejo y costoso, y sólo accesible a unos pocos Institutos Nacionales de Metrología (INM). La realización estaba basada en comparar la fuerza (peso) de una masa con la fuerza magnética entre dos bobinas por las que circula una corriente, conllevando una incertidumbre relativa en la realización del amperio del orden de partes en 10⁶. Una forma de mejorar la incertidumbre era mediante el denominado condensador calculable, en el que se establecía una relación entre la capacidad y la longitud (condensador de Thomson- Lampard  ([4, 5]), ligando entre sí la permitividad del vacío ε₀, la permeabilidad magnética del vacío µ₀ y la velocidad de la luz en el vacío c, mediante la expresión c² = 1 / µ₀ ε₀.

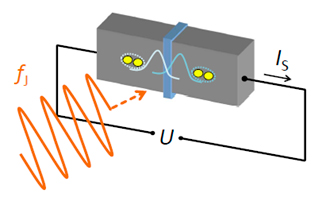
En la segunda mitad del siglo XX, con el descubrimiento de dos efectos cuánticos eléctricos macroscópicos, los efectos Hall cuántico y Josephson, comenzó un nuevo capítulo en la metrología eléctrica, y las técnicas conocidas hasta ese momento para la realización de la unidad eléctrica de acuerdo con su definición en el anterior SI pasaron a un segundo plano. Por una parte, Brian Josephson predijo teóricamente en 1962 una serie de efectos [6] que llevan su nombre y por los que fue galardonado con el Nobel de física en 1973. Estos efectos se producían entre superconductores débilmente acoplados, que constituyen una unión Josephson representada en la figura 3. Al irradiar una unión Josephson con una señal de muy alta frecuencia se produce una diferencia de tensión entre los dos superconductores dada por la siguiente expresión:

\(U=\frac{nf_{J}}{K_{J}}=\frac{h}{2e}nf_{J} ~ ~ ~ ~n=1,2,…\)     (2)

donde K_J es la constante de Josephson, n el número del escalón y f_J la frecuencia de microondas aplicada. Debido a la forma de la curva de corriente frente a tensión mostrada en la figura 4, se suelen denominar escalones a los distintos valores de tensión constante generados por una unión Josephson.

El efecto Josephson permite, por lo tanto, obtener valores de tensión que dependen sólo de dos constantes fundamentales, la carga elemental e y la constante de Planck h, y de la frecuencia de la radiación de microondas aplicada, que se puede medir con una incertidumbre muy baja, por lo que la tensión generada por este método tendrá una incertidumbre muy pequeña.

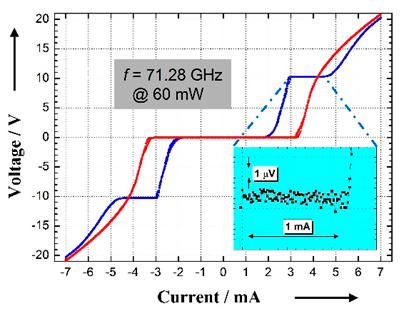
El segundo efecto cuántico que aparece en escena es el efecto Hall cuántico, observado experimentalmente en 1980 por Klaus von Klitzing [8] y que le valió la obtención del Nobel de física en 1985. Este efecto se produce en muestras semiconductoras bidimensionales. Al situar la muestra a temperaturas muy bajas, en torno a 1,4 K, y en campos magnéticos elevados, del orden de algunos teslas (~10 T), y aplicar una corriente, aparece una tensión transversal a la corriente aplicada, conocida como tensión Hall. Si se registran tanto la tensión Hall como la tensión longitudinal (en la misma dirección de la corriente) para distintos valores del campo magnético, se obtiene una curva como la de la figura 5. Como se puede observar en la figura 5, aparecen ciertas regiones o mesetas donde la curva es plana, y por lo tanto la tensión Hall permanece constante ante variaciones del campo magnético. En estas mesetas la resistencia Hall, definida como el cociente entre la tensión transversal y la corriente aplicada, tiene el siguiente valor:

\(R_{H}=\frac{1}{i}\frac{h}{e^{2}}=\frac{R_{K}}{i}~~~~i=(1,2,…)\)     (3)

donde R_K es la constante de von Klitzing, h es la constante de Planck, e la carga eléctrica elemental e i un número entero que indica la meseta.

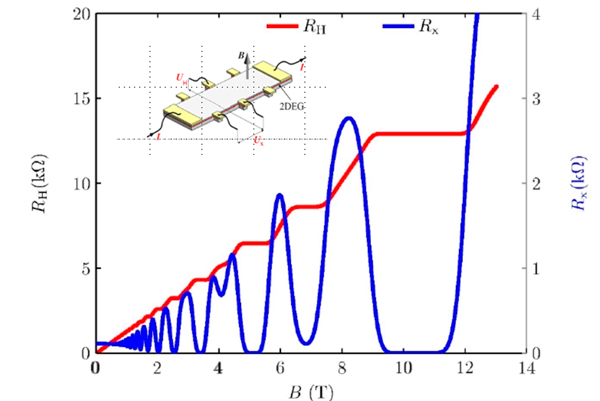
Por razones prácticas el Comité Internacional de Pesas y Medidas (CIPM) asignó en 1990 a las constantes R_K y K_J unos valores convencionales, R_K-90 y K_J-90, por lo que el amperio obtenido con la combinación de ambos efectos no era una realización en sentido estricto al no tener en cuenta la definición formal, sino solamente una representación de la unidad. Esto significó en la práctica crear un sistema artificial de unidades denominadas unidades eléctricas convencionales que estaban fuera del SI pero cuyas diferencias con éste eran conocidas.

3.- Redefinición del amperio en el actual SI

En el SI revisado, que entró en vigor el 20 de mayo de 2019, todas las unidades básicas se definen a partir de constantes con valores numéricos establecidos, en el caso del amperio a partir de la carga elemental e (figura 6), siendo su definición la siguiente:

El amperio, símbolo A, es la unidad SI de intensidad de corriente eléctrica. Se define al fijar el valor numérico de la carga elemental, e, en 1,602 176 634×10^-19, cuando se expresa en la unidad C, igual a A·s, donde el segundo se define en función de la frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, Δν_Cs.

En el SI revisado las constantes de Josephson y von Klitzing, K_J y R_K, tienen los valores exactos derivados de fijar los valores numéricos de la constante de Planck h y de la carga elemental e, y las unidades eléctricas derivadas voltio y ohmio obtenidas mediante los efectos Josephson y Hall cuántico, respectivamente, cuentan ya con realizaciones y no representaciones, como era el caso en el sistema eléctrico convencional de 1990. La transición del sistema eléctrico convencional al SI revisado supuso pequeños cambios en la diseminación de las unidades eléctricas, del orden de 0,1 partes por millón para el voltio y algo menores para el ohmio, que no afectaron a la mayoría de los usuarios.

Las unidades básicas en el nuevo SI se definen a partir de un conjunto de constantes fundamentales de la naturaleza que permanecen fijas, sin embargo el proceso de realización de las unidades puede cambiar para adaptarse a los avances científicos y tecnológicos. Esto permitirá que todas las unidades cuenten con realizaciones prácticas reproducibles en cualquier tiempo y lugar.

Esta nueva definición del amperio basada en la carga elemental no requiere ya las unidades mecánicas.

4.- Realización del amperio en el actual SI

Una ventaja de la nueva definición del amperio es que no especifica ningún tipo de realización, por lo que las realizaciones prácticas son elegibles, y reproducibles en cualquier tiempo y lugar. En [9] se proponen tres posibles realizaciones prácticas (“mise-en pratique”) para el amperio:

1. Basándose en la ley de Ohm A = V / Ω y las realizaciones prácticas de las unidades de tensión y resistencia basadas en los efectos Josephson y Hall cuántico, respectivamente.
   
2. Usando la relación que se produce en el proceso de carga de un condensador I = C dU / dt, la relación entre unidades A = F×V / s y las realizaciones prácticas de las unidades voltio V, faradio F y segundo s [10].
   
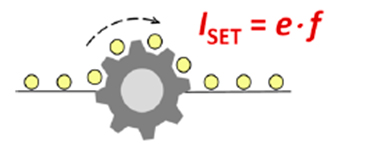
3. Usando el transporte individual de electrones (SET) (que se muestra de forma esquemática en la figura 7), contando el número de electrones por unidad de tiempo, la relación entre unidades A = C / s, el valor de la carga elemental e dado en la definición del amperio y la realización práctica de la unidad básica SI de tiempo, el segundo s. A pesar de que la implementación de esta técnica de recuento de electrones tiene todavía limitaciones técnicas, intensidades de corriente demasiado bajas para su aplicación práctica e incertidumbres mayores que las dos realizaciones anteriores, se incluye porque permite su realización de forma directa y sus incertidumbres están mejorando de forma considerable en los últimos años [11, 12]. La realización por este método permitirá cerrar el conocido como triangulo cuántico: tensión, resistencia e intensidad.

5.- Conclusiones

Las unidades básicas en el nuevo SI se definen a partir de un conjunto de constantes fundamentales de la naturaleza que permanecen fijas, sin embargo el proceso de realización de las unidades puede cambiar para adaptarse a los avances científicos y tecnológicos. Esto permitirá que todas las unidades cuenten con realizaciones prácticas reproducibles en cualquier tiempo y lugar. En el caso del amperio, la nueva definición basada en la carga elemental e independiza las unidades eléctricas de las mecánicas.

En el SI revisado las constantes de Josephson y von Klitzing, K_J y R_K, tienen los valores exactos, no convencionales, derivados de fijar los valores numéricos de la constante de Planck h y la carga elemental e, y las unidades eléctricas derivadas voltio y ohmio obtenidas con los efectos Josephson y Hall cuántico, respectivamente, son ya realizaciones y no representaciones, como era el caso en el sistema eléctrico convencional de 1990. La transición del sistema eléctrico convencional al SI revisado supuso pequeños cambios en la diseminación de las unidades eléctricas, del orden de 0,1 partes por millón para el voltio y algo menores para el ohmio, inapreciables en la vida cotidiana, únicamente la realización de ajustes en los valores de los patrones para medidas muy exactas.

6.- Referencias

[1] BIPM, The International System of units (SI), http://www.bipm.org/en/si/, Sèvres.

[2] W. Poirier, S. Djordjevic, F. Schopfer, O. Thévenot, The ampere and the electrical units in the quantum era, C. R. Physique 20 (2019), 92-128.

[3] P. Vigoureux, A determination of the ampere, Metrologia, 1 (1965), 3.

[4] S. Awan, B. Kibble, J. Schurr, Coaxial Electrical Circuits for Interference-Free Measurements, The Institution of Engineering and Technology, New York, 2011.

[5] A. M. Thompson y D. G. Lampard, «A New Theorem in Electrostatics and its Application to Calculable Standards of Capacitance,» Nature, vol. 177, pp. 888-888, 5 1956.

[6] B. D. Josepshon, Possible New Effects in Superconductive Tunnelling. Phys. Rev. Lett. 1 (1962) 251.

[7] J. Kohlmann and R. Behr, Development of Josephson voltage standards. Published: July 18th 2011. DOI: 10.5772/17031.

[8] K. von Klitzing, G. Dorda, M. Pepper, New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance, Phys. Rev. Lett. 45 (1980) 94.

[9] SI Brochure Mise en pratique for the definition of the ampere and other electric units in the SI – 9th edition (2019) – Appendix 2, 20 May 2019.

[10] D. Drung, C. Krause, U. Becker, H. Scherer and F. Ahlers, Ultrastable low-noise current amplifier: a novel device for measuring small electric currents with high accuracy, Rev. Sci. Instrum., 86 (2015), Article 024703.

[11] M. W. Keller, A. L. Eichenberger, J. M. Martinis and N. M. Zimmermann, A capacitance standard based on counting electrons, Science, 285, (1999), pp. 1706-1709.

[12] J.P. Pekola, O.P. Saira, V. Maisi, A. Kemppinen, M. Möttönen, Y.A. Pashkin and D. Averin, Single-electron current sources: toward a refined definition of the ampere, Rev. Mod. Phys., 85 (2013), pp. 1421-1472.