Alejandro Acquarone (LATU)
Carlos Galván Hernández (CENAM)
Ethel Beer (INTI)
Leonardo Rojas (LACOMET)
Liliana Álvarez (INTI)
Ricardo França (INMETRO)
En este trabajo se muestra el estado del arte en materia de mediciones de desviación de planitud en el ámbito del Sistema Interamericano de Metrología (SIM). A partir de un trabajo colaborativo entre institutos de metrología de la mencionada región ha sido posible no solo mejorar los sistemas de medición en dicha magnitud que actualmente se encuentran en operación, sino también lograr el emplazamiento de nuevos desarrollos interferométricos de diseño propio, logrando independencia tecnológica y que sientan las bases para el fortalecimiento del área de nanometrología en la región, permitiendo además la implementación de nuevas capacidades de medición y calibración. Por otro lado, la interacción ha permitido la generación de nuevos métodos de análisis de procesamiento de imágenes basado en filtros de Gabor aplicados a un único interferograma.
Palabras clave: desviación de planitud, interferómetro de Fizeau, metrología dimensional, filtros de Gabor.
This work shows the state of the art in terms of flatness deviation measurements at the Inter-American Metrology System (SIM). Some national metrology institutes of this region interacted through a project in order not only to improve the measurement systems which are currently in operation, but also to achieve the set-up of new interferometric developments of their own design, allowing the implementation of new measurement and calibration capabilities. This also allows reaching technological independence and strengthening the area of nanometrology in the region. On the other hand, a new method of image processing analysis based on Gabor filters applied to a single interferogram was developed.
Keywords: flatness deviation, Fizeau interferometer, dimensional metrology, Gabor filter.
1. Introducción
El método de medición de la desviación de planitud consiste en la comparación entre una superficie de referencia o patrón y la superficie de prueba a calibrar. Actualmente en el ámbito del Sistema Interamericano de Metrología (SIM), el Instituto Nacional de Metrología, Qualidade e Tecnología, INMETRO de Brasil, es el único instituto nacional de metrología (INM) de la región que tiene una capacidad de medición y calibración (CMC) declarada en medición de la desviación de planitud. Cuenta para ello con un interferómetro de Fizeau comercial que opera con una lámpara espectral de talio. Por otro lado el Instituto Nacional de Tecnología Industrial, INTI de Argentina, desde hace algunos años viene realizando este tipo de mediciones a partir de un interferómetro de Fizeau de diseño propio.
Con el objetivo de desarrollar nuevas capacidades de medición y dar trazabilidad al resto de los institutos nacionales de metrología (INM) del SIM en el campo de la nanotecnología, INMETRO e INTI iniciaron un trabajo colaborativo, que se enfocó inicialmente en la validación cruzada, automatización y mejora de sus sistemas interferométricos de medición de la desviación de planitud. A través de la financiación externa del Banco Interamericano de Desarrollo (BID) de un proyecto de investigación, ha sido posible extender esta colaboración a otros INM de la región. Así es como, además de los institutos anteriormente mencionados, actualmente participan de este proyecto: el Centro Nacional de Metrología, CENAM de México, el Laboratorio Tecnológico del Uruguay, LATU y el Laboratorio Costarricense de Metrología, LACOMET. La idea de este trabajo en conjunto es, por un lado, fortalecer los lazos entre los INM de la región, mediante el intercambio de experticias técnicas, así mismo la transferencia de tecnología y conocimiento generada por este proyecto queda a disposición del resto de los INM del SIM. Por otro lado, este proyecto proporciona una base para el inicio de comparaciones en la desviación de planitud y colaboración entre INM pertenecientes al SIM así como con el resto de la comunidad internacional de metrología.
2. Descripción de los dispositivos experimentales
La determinación de la desviación de planitud generalmente se realiza a partir de técnicas ópticas o métodos interferométricos. Esta técnica requiere de una superficie de referencia previamente calibrada contra la cual se comparará la pieza bajo calibración. Una configuración posible para este tipo de medición es a través de un interferómetro de Fizeau, como el que se esquematiza en la Figura 1. En este caso la fuente de iluminación utilizada es una lámpara de vapor de sodio o una lámpara de vapor de mercurio a baja presión o una lámpara de descarga de helio o incluso bajo ciertas condiciones podría utilizarse una lámpara de tungsteno [1, 2]. Dependiendo del tipo de fuente de iluminación utilizada, la correspondiente longitud de coherencia permitirá separar físicamente o no, las caras bajo ensayo. Cuando se utilizan dos planos ópticos “perfectos”, uno de los cuales corresponde a un patrón de planitud, ambas superficies no estarán exactamente paralelas generándose un gradiente de espesor entre ellas. Las reflexiones en estas superficies se superponen en el divisor de haz dando lugar a un patrón de interferencia como el indicado en la Figura 1.
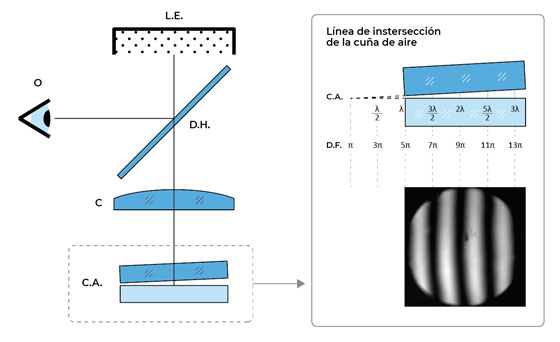
Uno de los sistemas interferométricos utilizado por INMETRO para la determinación de la desviación de planitud corresponde a este tipo de configuración en la cual se utiliza una lámpara de talio con longitud de onda de 535,046 nm en el vacío. Este sistema ha sido adaptado para el registro de la imagen digital.
Otra configuración posible de este tipo de interferómetro se esquematiza en la Figura 2, la cual utiliza como fuente de iluminación un sistema láser. Dada la longitud de coherencia de la fuente de iluminación, en este caso, es posible trabajar con un gradiente de espesor aún mayor que el considerado en el interferómetro de Fizeau descrito anteriormente, separando así físicamente los planos ópticos, patrón y bajo calibración, a costa de requerir condiciones más estrictas de colimación y de tamaño de fuente, [1-3].
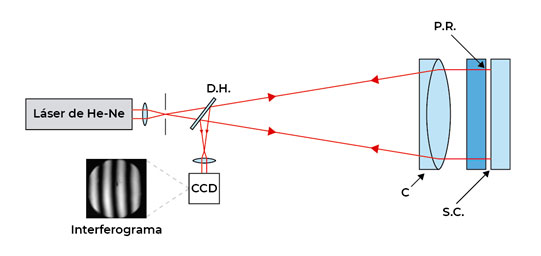
En este caso mediante un ajuste fino para regular la posición del plano óptico bajo calibración es posible controlar el número de franjas de interferencia y su dirección, lo que permite la determinación de la máxima desviación de planitud de la superficie ensayada. El interferómetro que opera INTI es un diseño propio basado en esta configuración, que utiliza un láser de He-Ne con una emisión de 632,8 nm en el vacío.
Desde hace algunos años y a raíz de los avances tecnológicos ha surgido una nueva generación de interferómetros basados en técnicas de desplazamiento de fase (PSI, phase shifting interferometry) [4]. Esta técnica no resulta exclusiva del campo de la óptica, ya que resulta un método de adquisición y análisis de datos que puede aplicarse en otras áreas. El método por desplazamiento de fase requiere del registro de una serie de interferogramas, en los cuales se va modificando la fase de referencia del interferómetro, introduciendo un desplazamiento de fase constante, que puede ser conocido o no. Existen diversas técnicas para lograr dicho desplazamiento de fase, siendo esta la más difundida, mediante un posicionador nanométrico, en el cual se monta el plano óptico de referencia. La principal ventaja de este método frente al descrito anteriormente, es que permite la determinación de la desviación de planitud en cada punto de la superficie bajo calibración.
Actualmente INMETRO cuenta con un interferómetro comercial con técnicas de PSI para la calibración de bloques patrón, que también permite la calibración de la desviación de planitud incorporando esta técnica. Por su parte INTI ha realizado mejoras en su interferómetro de Fizeau que incluyen la incorporación de un sistema para la generación de desplazamiento de fases. En el marco de este proyecto se viene trabajando en conjunto en la optimización de los algoritmos utilizados por ambos institutos, y con la evaluación de las contribuciones a las incertidumbres de medición correspondientes.
Existen diversos métodos, tanto relativos como absolutos, para la determinación de planitud. En este trabajo nos concentramos en aquellos basados en técnicas de interferometría.
3. Métodos relativos
Estos tipos de métodos se basan en la medición del espesor de la capa formada entre ambas superficies planas [2]. Las franjas de interferencia generadas a partir de un interferómetro de Fizeau se denominan franjas de igual espesor, ya que dependen de un gradiente de espesor óptico. Los interferogramas obtenidos a partir de dichos sistemas, resultan en un patrón de intensidad que responden matemáticamente a la siguiente expresión:
\(I\left(x,y\right)=a\left(x,y\right)+b\left(x,y\right)\cos{\left(\varphi\left(x,y\right)\right)}\)
(1)
donde \(I\left(x,y\right)\)
es la distribución de intensidad que registra la cámara en cada pixel de coordenadas \(\left(x,y\right)\)
,
\(a\left(x,y\right)\) contiene todas las contribuciones aditivas o intensidad de fondo, \(b\left(x,y\right)\)
corresponde a contribuciones multiplicativas asociadas a la modulación, y
\(\varphi\left(x,y\right)\) es la fase entre los haces que interfieren y que codifica la magnitud física que se pretende determinar, que en este caso es la desviación de planitud. Cabe señalar que un detector ideal realiza una conversión lineal de la intensidad en una señal eléctrica.
Para la configuración del interferómetro de Fizeau, descrito en la sección anterior, la diferencia de camino óptico se genera a partir de las irregularidades, \(\xi\left(x,y\right)\), de la superficie bajo ensayo comparada con el patrón de planitud calibrado. En este caso \(\left(x,y\right)\) representan las coordenadas espaciales en dicha superficie. Así para incidencia aproximadamente normal, la fase del frente de onda y las irregularidades de la superficie se relacionan mediante:
\(\varphi\left(x,y\right)=\ \frac{4\pi}{\lambda}\ \xi\left(x,y\right)\)
(2)
En las técnicas de interferometría el objetivo es decodificar y extraer \(\varphi\left(x,y\right)\) a partir de la distribución de intensidad para lo cual existen diferentes métodos posibles.
3.1 Máxima tolerancia
Una forma de evaluar y verificar la planitud de una superficie consiste en modificar la posición relativa de la superficie bajo calibración respecto de la superficie de referencia, de manera tal que se visualice en el campo del interferograma el interior de un único orden de interferencia. Bajo esta condición es posible asegurar que la desviación de planitud de la superficie se encuentre por debajo de λ/4, donde λ es la longitud de onda de la fuente utilizada. En este caso se evalúa si la superficie ensayada cumple o no con la especificación establecida.
Normalmente este método resulta apropiado para el ensayo de paralelas ópticas y cristales de interferencia de trabajo utilizados, por lo general, para la calibración de micrómetros. La incertidumbre que puede alcanzarse en este caso está caracterizada por la especificación de la superficie de referencia. Así por ejemplo, si el patrón de planitud considerado tiene una especificación de λ/20, la incertidumbre asociada a la determinación de la desviación de planitud por tolerancia será de \(2\ast\frac{\lambda}{(\sqrt3\ \ \ast\ 20)}\) para un factor de cobertura k = 2.
3.2 Determinación de la máxima desviación de planitud
Una manera de determinar la máxima desviación de planitud de la superficie bajo calibración, a partir de un interferograma, consiste en evaluar la máxima desviación o sagita, F, (también denominada flecha) de las franjas del patrón de interferencia y la correspondiente distancia interfranja, I, (Figura 3). Esto puede realizarse mediante inspección visual y con la ayuda de un sistema óptico equipado con una regla graduada, o mediante un sistema de detección automática. En este último caso la información en intensidad del interferograma se digitaliza mediante una cámara.
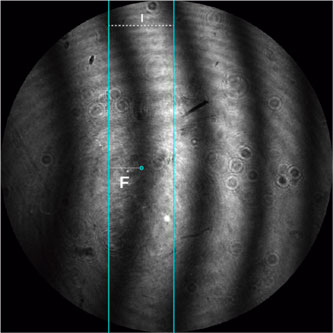
De acuerdo a la norma de referencia utilizada [5], la desviación máxima de planitud en el campo visual del interferograma examinado, se determina a través de:
\(\xi_{max}=\frac{F}{I}\frac{\lambda}{2}\)
(3)
donde ξmáx es la desviación máxima de planitud, F es la deflexión máxima o sagita, I es la interfranja, y λ es la longitud de onda.
Existen dos maneras de realizar el relevamiento y determinación de la sagita y la distancia interfranja:
- Manteniendo el número de franjas de interferencia en el campo visual y variando la posición angular del patrón de planitud en, por ejemplo, ocho posiciones tal como se realiza en INMETRO. Los valores de sagita e interfranja se promedian y se reemplazan en (3).
- Variando el número de franjas de interferencia en el campo visual entre tres o cuatro franjas de mínima y hasta quince. Con las determinaciones de sagita e interfranjas se realiza una regresión lineal. La pendiente de la recta de ajuste se reemplaza en la ecuación (3). Esta metodología de trabajo se realiza en INTI.
Mediante un largo y exhaustivo trabajo comparando distintos planos ópticos entre INMETRO e INTI, se ha demostrado que ambas metodologías resultan equivalentes.
La incertidumbre que se alcanza con estos métodos depende por un lado de la incertidumbre en la determinación de la sagita, y la distancia interfranja, o de la incertidumbre en la determinación del parámetro de la pendiente de la mejor recta que ajuste dichos datos, según el caso i) o ii) respectivamente. La contribución más importante en este método corresponde a la incertidumbre asociada al patrón de planitud. Dicha incertidumbre se puede considerar tomando la incertidumbre de calibración de dicho patrón de planitud, o considerando el valor de planitud medida en forma absoluta y su incertidumbre, de acuerdo a lo que se describe en 3.4. La incertidumbre asociada a la contribución de la longitud de onda y su corrección por índice de refracción resultan despreciables frente al resto de las fuentes de incertidumbres descritas. Los valores típicos de incertidumbres para este método resultan del orden de los 30 nm, para un factor de cobertura k = 2.
3.3 Determinación de la topografía
El objetivo es descodificar y extraer valores de fase a partir de la distribución de intensidad descrita por la ecuación (1), y obtener a partir de esta magnitud el valor de la desviación de planitud en cada punto de la superficie bajo calibración utilizando la ecuación (2), es decir se obtiene en este caso un mapa topográfico de la superficie comparada con el patrón de planitud.
Existen distintos métodos y algoritmos para la recuperación de la fase [6, 7, 8], tales como el método de Fourier, el de regularización o el método de descomposición de modo empírico bidimensional, que utilizan un único interferograma estático y se basan en la localización de los centros de las franjas de interferencia. Otro método, cuya aplicación no se limita solo al campo de la óptica, es el de escalonamiento o desplazamiento de fase o PSI (de las siglas en inglés phase stepping/shifting interferometry) a través del cual se realiza el registro de una serie de interferogramas en los cuales se introduce una fase portadora.
La forma más clásica para introducir la fase portadora es mediante el movimiento de uno de los componentes ópticos. En el caso del interferómetro de Fizeau la aplicación de esta técnica se realiza generalmente desplazando uno de los planos ópticos mediante un trasladador piezoeléctrico. La distribución de intensidad descrita por la ecuación (1) puede reescribirse de la siguiente manera [9]:
\(I_{i}\left(x,y\right)=I_{0}\left(x,y\right)\left \{1+\gamma\left(x,y\right)\ cos\left[\varphi\left(x,y\right)+\delta_{i}\right]\right \}\)
(4)
donde \(I_{i}\left(x,y\right)\) es la intensidad en
\(\left(x,y\right)\) en el detector,
\(I_{0}\left(x,y\right)\) es la intensidad promedio, \(\gamma\left(x,y\right)\) es la visibilidad de las franjas de interferencia,
\(\varphi\left(x,y\right)\) es la fase a ser medida y
\(\delta_{i}\) es el desplazamiento de fase aplicado en el i-ésimo interferograma. Las incógnitas en esta ecuación son I0, γ,
y φ de donde se deduce que para poder determinar la fase se necesita como mínimo registrar tres interferogramas. En la actualidad existen varios algoritmos posibles con un número variado de interferogramas y para diversos valores de pasos y fase inicial [1,4].
Los interferómetros comerciales que operan con este tipo de técnica suelen emplear el algoritmo basado en 5 registros de intensidad cuya eficiencia ha sido vastamente estudiada, y demostrado que resulta insensible a errores de tipo sistemático. Para pasos de fase \(\delta_{i}=\left(i-1\right)\frac{\pi}{2}\) la fase se determina:
\(\varphi\left(x,y\right)=\ {\mathrm{tan}}^{-1}\left\{\frac{2\ \left[I_4\left(x,y\right)-I_2\left(x,y\right)\right]}{I_1\left(x,y\right)-2I_3\left(x,y\right)+I_5\left(x,y\right)}\right\}\)
(5)
La determinación de la desviación de planitud punto a punto se realiza combinando el mapa de fase obtenido de la ecuación (5) y la ecuación (2). La Figura 4 muestra un resultado típico obtenido por esta técnica.
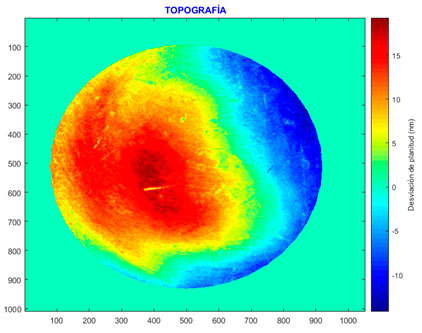
La precisión del método mejora cuanto mayor es el número de interferogramas considerados y cuando el número de franjas se reduce al mínimo, ya que se reduce la componente por inclinación y no es necesario aplicar técnicas de desenvolvimiento de fase. Dentro de las contribuciones a la incertidumbre de este método se destaca por un lado la calibración de la técnica de desplazamiento de fase utilizada para introducir la fase relativa entre los interferogramas, por ejemplo, para el caso del trasladador piezoeléctrico sería la linealidad. La contribución de mayor relevancia es la incertidumbre del patrón de planitud utilizado en la medición [9]. Las contribuciones asociadas al detector con el cual se realizan los registros y a la longitud de onda y su corrección por índice de refracción resultan despreciables. Los valores típicos de las incertidumbres asociadas a estas técnicas tanto para un interferómetro comercial (INMETRO) como uno de diseño propio (INTI) alcanzan los 20 nm, con factor de cobertura k = 2.
4. Métodos absolutos
La realización de la planitud merece ciertas consideraciones especiales. Como se mencionó anteriormente la medición de esta magnitud consiste en comparar una superficie que se asume como plana en el sentido matemático contra un patrón, cuyas desviaciones de un plano matemático ideal también deben ser medidas. Contar con este tipo de métodos es importante ya que permite la calibración de las referencias de planitud, evitando así la necesidad de depender de calibraciones externas y hace posible cerrar la cadena de trazabilidad en el propio laboratorio. En este sentido se presentan en este trabajo dos métodos absolutos que actualmente se están desarrollando en INMETRO e INTI.
4.1 Superficies líquidas
En este caso se utiliza como plano material la superficie libre de un líquido, que actúa como patrón de planitud [10, 11]. Dada la propiedad de los líquidos de esparcirse es posible asumir que todos los puntos que componen su superficie tienen el mismo potencial gravitatorio, es decir se encuentran físicamente en un mismo plano. Esto a su vez requiere que el plano a calibrar sea colocado en posición horizontal, con lo cual, el interferómetro a utilizarse deberá ser de configuración vertical. Dependiendo del líquido empleado existen diversos factores que afectan a la medición tales como por ejemplo: las vibraciones y perturbaciones externas, la frecuencia natural de oscilación del sistema, corrientes de aire, efectos térmicos, efectos gravitatorios, reflectancia de la superficie, etc.
Actualmente INMETRO está trabajando en la implementación de esta técnica para lo cual se adapta el interferómetro comercial incorporando como superficie líquida de referencia un aceite (Figura 5). La medición de la desviación de planitud se realiza siguiendo lo descrito en 3.2.

4.2 Método de los tres planos
Es posible medir planitud en forma absoluta sin utilizar un patrón absoluto. El método tradicional asume que la forma de las superficies es independiente del tiempo y la posición, con lo cual es posible colocar los planos a medir en posición vertical, utilizando un interferómetro de configuración horizontal. [10, 12]. El método requiere la utilización de tres planos cuyas desviaciones se pretenden determinar, y que se miden uno contra otro, de acuerdo a las configuraciones indicadas en la Figura 6.
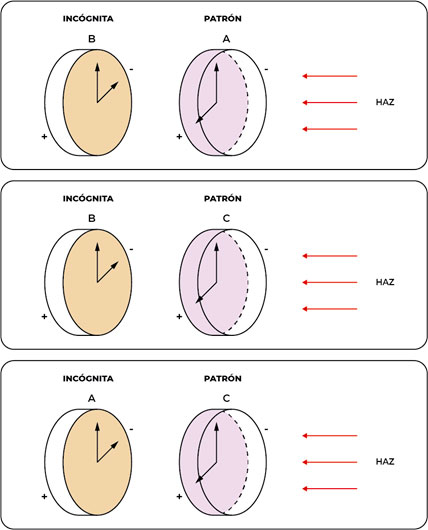
A partir de estas configuraciones, se plantea un sistema de tres ecuaciones con tres incógnitas:
\(B+\ A=\ \zeta_{BA}\)
\(B+\ C=\ \zeta_{BC}\)
\(A+\ C=\ \zeta_{AC}\)
(6)
donde A, B y C describen la desviaciones de planitud individuales de cada superficie, que se desea determinar, y \(\zeta_{BA}\), \(\zeta_{BC}\)
y \(\zeta_{AC}\) son las desviaciones de planitud relativas, medidas interferométricamente. Resolviendo el sistema de ecuaciones (6) se obtienen las desviaciones de planitud individual:
\(A=\ \frac{-\zeta_{BA}+\zeta_{BC}+\ \zeta_{AC}}{2}\)
\(B=\ \frac{\zeta_{BA}+\zeta_{BC}-\ \zeta_{AC}}{2}\)
\(C=\ \frac{\zeta_{BA}-\zeta_{BC}+\ \zeta_{AC}}{2}\)
(7)
Se puede demostrar que la incertidumbre asociada a estas mediciones absolutas es \(u\left(\zeta_{abs}\right)=\frac{\sqrt3}{2}u\left(\zeta_{rel}\right)\), donde \(u\left(\zeta_{rel}\right)\) es la incertidumbre de medición del método relativo, asociada al modelo de las ecuaciones (6).
Este método tradicional de la técnica de los tres planos no permite la determinación de la desviación de planitud punto a punto en toda la superficie, ya que, como se mencionó anteriormente el planteo del sistema de ecuaciones (6) asume que existe simetría de rotación. Existen otras variantes de esta técnica que consideran rotaciones sucesivas, fijas o arbitrarias, a fin de tratar las asimetrías presentes en las superficies analizadas [10, 12].
Una de las mejoras efectuadas en el sistema de medición de planitud de INTI, consiste en la aplicación del método de los tres planos tradicional para la medición absoluta de sus referencias de planitud, logrando así cerrar la cadena de trazabilidad en el laboratorio.
5. Resultados más relevantes
5.1 Nuevos emplazamientos
Uno de los resultados más importantes a destacar es la transferencia de tecnología. Existen muchos aspectos que hacen al logro de este objetivo alcanzado, siendo el más tangible el montaje de nuevos dispositivos experimentales. Tal es el caso del nuevo desarrollo de sistema interferométrico en LACOMET, Figura 7.

La puesta a punto de este sistema se realizó desde cero, contando con una inversión para la adquisición del equipamiento correspondiente, y la implementación de nuevas técnicas de medición basadas en interferometría, y que aplica el método de máxima desviación de planitud, descrito en 3.2. Para la validación del software se utilizaron series de imágenes generadas por los otros sistemas de medición del SIM. Actualmente se plantea la necesidad de comparaciones de este nuevo sistema con los ya existentes en la región.
Este sistema permitirá el desarrollo de nuevas capacidades de medición y calibración, en desviación de planitud, de suma importancia para cubrir la demanda de la industria de la región y sienta las bases para futuros desarrollos en el área de la nanometrología.
5.2 Desarrollo de nuevos métodos de análisis
Otro aspecto de gran importancia es el desarrollo de nuevos métodos de análisis basados en un único interferograma. Los interferómetros de INMETRO y el recientemente desarrollado en LACOMET, realizan la medición de esta forma por eso es importante el desarrollo de métodos de análisis con una sola imagen.
Un método propuesto está basado en Filtros de Gabor, en esta propuesta se hace uso de un banco de filtros alrededor de la frecuencia portadora del interferograma y con distintas orientaciones y se evalúa la respuesta de los filtros en cada punto del interferograma.
Una función de Gabor 2-D, es una función armónica (una retícula sinusoidal, por ejemplo) en el dominio de los complejos, la cual modula a una función Gaussiana, lo que puede expresarse como:
\(h\left(x,y\right)=g\left(x^\prime,y^\prime\right)exp\left(j2\pi F\ x^\prime\right)\)
(8)
donde \(\left(x^\prime,y^\prime\right)=\left(x\cos{\emptyset}+y\sin{\emptyset,}x\ \sin{\emptyset}\ -y\cos{\emptyset}\right)\) son las coordenadas espaciales rotadas y \((F,\emptyset)\) son la frecuencia central y la orientación, las cuales definen el filtro en dominio del espacio, \(g\left(x,y\right)\)
es una función gaussiana:
\(g\left ( x,y \right ) = \frac{1}{2\pi\sigma_x\sigma_y}exp\left[-0.5\left(\frac{x^2}{{\sigma_x}^2}+\frac{y^2}{{\sigma_y}^2}\right)\right]\)
(9)
\(\left (\sigma_{x},\sigma_{y} \right )\) representan el ancho de banda de la Gaussiana, y por lo tanto el ancho de banda del filtro. Este filtro puede ser entonado en una frecuencia específica y orientación
; lo anterior permite que se pueda crear un banco de filtros variando la frecuencia y la orientación, en la Figura 9, se muestra la parte real de los filtros obtenidos para 6 orientaciones y 6 frecuencias [13].

Para el algoritmo propuesto, la frecuencia se determina usando la transformada discreta de Fourier, y los filtros son generados alrededor de esta frecuencia, la orientación inicial se obtiene como la tangente de las componentes horizontal y vertical de las frecuencias. Después de aplicar el banco de filtros al interferograma, se determina para cada posición cuál de los filtros contiene la respuesta máxima, la fase de este filtro es colocada como la fase para ese punto. Con este análisis se obtiene el mapa de fase envuelta para el interferograma. La Figura 10 muestra el interferograma real y los resultados obtenidos usando 16 orientaciones y 3 frecuencias, es decir un banco de 48 filtros.

En los resultados se puede observar la eliminación tanto de ruido como de las variaciones de intensidad en el interferograma. Con estos resultados, y dado que está montado sobre una frecuencia portadora dominante, se puede estimar ese plano como la mediana de la gradiente de la fase, tanto en dirección X como en dirección Y; al eliminar este plano de la fase envuelta se puede obtener una buena aproximación del mapa de fase, ver la Figura 11.
Una de las ventajas de este método, es que puede definir los pasos de la fase para los filtros de Gabor, tan fino como se requiera, claro que esto impacta en el tiempo de procesamiento.

Como continuación de este desarrollo, se planea el empleo de modelos de regularización para afinar los detalles; los resultados obtenidos con el método de Gabor serán usados como punto de arranque para un algoritmo basado en el modelo de regularización [7], donde se espera obtener el modelo de fase sin discontinuidades derivado de los pasos en los filtros de Gabor; adicionalmente los elementos de iluminación del modelo general de interferencia podrán ser recuperados.
5.3 Otros resultados y perspectivas a futuro
A fin de extender la transferencia de tecnología al resto de los institutos nacionales de metrología que conforman el SIM, se tiene prevista la realización de un seminario/taller de metrología óptica, apuntando principalmente a la puesta en marcha de sistemas interferométricos como los descritos.
Por otro lado, el desarrollo del proyecto de investigación ha facilitado la posibilidad de una comparación bilateral entre INMETRO e INTI, la cual se encuentra actualmente en preparación. Esto es sumamente importante para la región del SIM, ya que es la primera comparación de desviación de planitud que se realiza en dicho ámbito regional. Así mismo y a partir de la transferencia de tecnología lograda, y la que se tiene prevista a futuro, se espera establecer un sistema de comparaciones en esta magnitud que trascienda la región de las Américas.
6. Conclusión
En este trabajo se han presentado diversos aspectos que hacen a las mediciones de desviación de planitud desarrolladas actualmente en el ámbito del Sistema Interamericano de Metrología, SIM, a partir de un trabajo en conjunto de colegas de cinco institutos de metrología de la mencionada región. Fundamentalmente se ha trabajado sobre sistemas interferométricos ya existentes para su mejora y extensión de capacidades de medición. Esto ha permitido la concreción de nuevas comparaciones en la magnitud de desviación de planitud en la región, lo cual era una falencia importante. Todo lo desarrollado permite fortalecer y sentar las bases para futuros desarrollos en el área de la nanometrología.
Por otra parte, la interacción ha permitido no solo la implementación de nuevas técnicas y algoritmos de medición sino también la transferencia de tecnología de las técnicas de medición basadas en interferometría, las que pretenden hacerse extensivas al resto de los institutos del SIM. Esto posibilita la declaración de nuevas CMC, y a su vez, refuerza el sistema de comparaciones en desviación de planitud en el SIM.
Dentro de las mejoras logradas, se destaca también la implementación de métodos absolutos de medición de desviación de planitud, lo cual garantiza la independencia de calibraciones externas, cerrando la cadena de trazabilidad en el laboratorio. Finalmente se concluye acerca de la ventaja de contar con sistemas de desarrollo propio lo cual garantiza cierta independencia tecnológica y el acceso al know how, frente a la de equipos comerciales llave en mano.
Todas estas actividades se desarrollaron en el marco de un proyecto de investigación BID-SIM: ATN N°15264-RG, “Fortalecimiento de los Institutos Nacionales de Metrología en el hemisferio, en respaldo de las Tecnologías Emergentes”, por lo que se destaca la importancia de contar con sistemas de financiamiento externos a los institutos, particularmente, en la región del SIM.
7. Referencias
[1] Malacara, D. (ed.). Optical shop testing. John Wiley & Sons, 2007.
[2] Hecht, E; Zajac A. Optica. Addison & Wesley Iberoamericana, 1986.
[3] Malacara, D.; Malacara, Z.; Servin, M. Interferogram analysis for optical testing. Taylor & Francis, 2005.
[4] Kreis, T. Holographic interferometry principles and methods. En Simulation and Experiment in Laser Metrology: Proceedings of the International Symposium on Laser Applications in Precision Measurements Held in Balatonfüred/Hungary. 1996.
[5] JIS B7430-1977. Optical Flats. Japanese Industrial Standard.
[6] Takeda, M. Spatial-carrier fringe-pattern analysis and its applications to precision interferometry and profilometry: an overview. Industrial Metrology, 1990, vol. 1, no 2.
[7] J. L. Marroquin, M. Rivera, S. Botello, R. Rodriguez-Vera, and M. Servin, “Regularization methods for processing fringe pattern images,” Appl. Opt. 38, 788–794 (1999).
[8] Dong, W., et al. A bidimensional empirical mode decomposition method for fusion of multispectral and panchromatic remote sensing images. Remote Sensing, 2014, vol. 6, no 9.
[9] Creath, K. Error sources in phase-measuring interferometry. En Intl Symp on Optical Fabrication, Testing, and Surface Evaluation. International Society for Optics and Photonics, 1992. p. 428-435.
[10] Schulz, G.; Schwider, J. Precise measurement of planeness. Applied Optics, 1967, vol. 6, no 6, p. 1077-1084.
[11] Moreno, A., et al. Calibración absoluta de un interferómetro Fizeau mediante un plano líquido. Simposio de Metrología, 2004.
[12] Fritz, B. Absolute calibration of an optical flat. Optical Engineering, 1984, vol. 23, no 4, p. 234379.
[13] Rivera Mariano, Dalmau Óscar, Gonzalez Adonai, Hernández López Francisco, Two-step fringe pattern analysis with a Gabor filter bank, Optics and Lasers in Engineering, vol. 85 [online first], p. 29-37, issn 0143-8166, doi 10.1016/j.optlaseng.2016.04.014, 2016
8. Agradecimientos
El desarrollo de este trabajo fue financiado por proyecto SIM-BID (ATN N°15264-RG) “Fortalecimiento de los Institutos Nacionales de Metrología en el hemisferio, en respaldo de las Tecnologías Emergentes” (Componente 1: Proyecto de Investigación Conjunta/Subcomponente 01.01.00).
Agradecemos muy especialmente al Dr. Mariano Rivera, del Centro de Investigación en Matemáticas (CIMAT, México), por su apoyo y valiosa colaboración en relación al diseño de algoritmos de procesamiento de interferogramas, con quien se mantuvieron valiosas discusiones. Así mismo agradecemos al Bach. Quim. Pablo Constantino (LATU) por su constante apoyo en temas de tratamiento de incertidumbre por método de Monte Carlo, y al Sr. Sebastián Pérez (INTI) por el soporte de edición gráfica.









Comentarios