Alberto Mínguez Martínez
Jesús de Vicente y Oliva
Escuela Técnica Superior de Ingenieros Industriales
Universidad Politécnica de Madrid
Resumen
Vivimos en un mundo en el que está muy extendido el concepto de la Industria 4.0. Uno de los objetivos de la Industria 4.0 es la obtención de pequeños lotes de productos con un alto grado de personalización. Los nuevos desarrollos han llevado a la miniaturización de sistemas y a la fabricación de piezas con dimensiones por debajo del milímetro en los entornos industriales. Cuando los fabricantes quieren estudiar la calidad de su producción, la miniaturización ha hecho que tengan que hacer frente a conceptos como incertidumbre de medida, calibración y trazabilidad. La Metrología Dimensional (DM) juega un papel crucial en el nuevo entorno de producción. Los instrumentos de medida más extendidos que nos permiten realizar medidas precisas a estas escalas son los microscopios ópticos, ya sean microscopios tradicionales, confocales, de variación de foco, proyectores de perfiles, o cualquier otro sistema de medida con un principio de funcionamiento similar.
Como metrólogos, nuestro principal deber es proporcionar una trazabilidad adecuada a las medidas realizadas con los diferentes instrumentos de medición. Sin embargo, el hecho de dotar de trazabilidad a la unidad de longitud del SI (el metro), a las medidas dimensionales 2D y 3D a escala micro y nano, está aún en estudio. En este artículo, los autores proponen un procedimiento para la calibración de las escalas de los instrumentos ópticos de medición, particularizando para un microscopio confocal, pero que puede usarse para la calibración de otros instrumentos de medición óptica, aplicando cambios menores.
La calibración se realizará utilizando patrones fáciles de encontrar y calibrar en laboratorios de metrología y calidad en entornos industriales. Como resultado complementario, se dotará de trazabilidad al parámetro de rugosidad Ra.
Abstract
We live in a world in which the concept of Industry 4.0 is increasingly widespread. One of the objectives of Industry 4.0 is obtaining small batches of products with a high degree of customization. On the other hand, new developments have led to the miniaturization of systems and the manufacture of parts with dimensions below the millimeter in industrial environments. When manufacturers want to study the quality of their production, miniaturization has meant that concepts such as measurement uncertainty, calibration and traceability must be addressed. Dimensional Metrology (DM) plays a crucial role in the new production environment. The most widespread measuring instruments that allow us to make precise measurements at these scales are optical microscopes, whether they are traditional microscopes, confocal, focus variation microscopes, profile projectors, or any other measurement system with a similar operating principle.
As metrologists, our main duty is to provide adequate traceability to the measurements made with the different measuring instruments. However, the fact of providing traceability to the length unit of the SI (the meter) to 2D and 3D dimensional measurements at the micro and nano scale is a problem that is being studied yet. In this article, the authors propose a procedure for the calibration of the scales of optical measuring instruments, particularizing for a confocal microscope, but able to be used for the calibration of other optical measuring instruments, applying minor changes.
The calibration will be accomplished using material standards easy to find and calibrate in metrology and quality laboratories in industrial environments. As a complementary result, the roughness Ra parameter will also be traced to the SI.
1. INTRODUCCIÓN
Una de las tendencias que existen a nivel industrial es la miniaturización de sistemas (1), es decir, el diseño, desarrollo y fabricación de componentes con dimensiones inferiores al milímetro. La miniaturización nació a finales de la década de 1960 y principios de la de 1970 con la revolución electrónica, cuando sistemas electrónicos, como los de radio o televisión, fueron desarrollados (2; 3). Hoy en día, la miniaturización de componentes es común a nivel industrial. Muchas de las nuevas tecnologías de fabricación como los procesos láser, los procesos de moldeo y de perforación a escala micro- o los procesos de haz de iones focalizado tienen su origen en procesos de fabricación tradicionales (3), que tuvieron que adaptarse para poder fabricar piezas con estas dimensiones.
En 2011, el gobierno de Alemania desarrolló el término Industria 4.0, que se entiende como la aplicación e integración de los sistemas ciber-físicos dentro de la producción industrial (4). Uno de sus objetivos, desde el punto de vista de la fabricación, es desarrollar productos con un alto grado de personalización y cortos ciclos de vida en el mercado, de manera rentable (5). Por ello, conceptos como el de Prototipado Rápido (RP) o Fabricación Aditiva (AM) son cada vez más frecuentes puesto que permiten obtener modelos de los productos que se quieren fabricar de una manera rápida y económica (6; 7). Uno de los pasos del proceso de producción es el control de calidad de los productos, en el que está incluida una verificación dimensional que busca evaluar si las piezas son conformes con las especificaciones de diseño. Debido a esto, los fabricantes han tenido que enfrentarse a conceptos como incertidumbre, calibración y trazabilidad metrológica (8), definidos en el VIM (9) en las secciones 2.25, 2.39 y 2.41 respectivamente.
1.1. Metrología de Coordenadas
Una de las técnicas más extendidas en el campo de la metrología dimensional es la metrología de coordenadas (CM), que consiste en determinar las coordenadas espaciales de elementos y superficies de piezas. Los instrumentos de medida que funcionan siguiendo este principio son las Máquinas de Medición por Coordenadas (CMMs) (10). Con una CMM es posible llevar a cabo un gran número de tareas metrológicas diferentes. Sin embargo, asegurar la trazabilidad de los resultados de medida obtenidos por las CMMs no es una tarea fácil (11; 12). Para dotar de trazabilidad a las tareas metrológicas de una CMM existen varias alternativas normalizadas (13):
- ISO 15530-3:2011 (14), donde se propone usar los Sistemas de Medición por Coordenadas (CMSs) básicamente como comparadores; es decir, comparando las medidas obtenidas sobre el mensurando con las medidas obtenidas sobre un patrón calibrado y estimar la incertidumbre a partir de la diferencia entre los resultados de medida obtenidos y los valores de calibración del patrón.
- ISO 15530-4:2011 (15), donde se propone utilizar un software de evaluación de la incertidumbre (UES), basado en un modelo matemático del proceso de medida. En el modelo, el proceso de medición se representa teniendo en cuenta los factores más importantes que influyen en la medida. En la simulación, todos estos factores de influencia se hacen variar dentro de su rango supuesto de valores, y dentro de distribuciones de probabilidad asignadas a priori, y el proceso de medición se simula utilizando todas las combinaciones posibles de las magnitudes de influencia. Finalmente, la incertidumbre se estima a partir de la variación observada del resultado.
- ISO/DTS 15530-2:2011 (16; 17), donde se describe un procedimiento para estimar la incertidumbre de una tarea de medición específica utilizando varias piezas de trabajo. Las mediciones se realizan en diferentes orientaciones y ubicaciones, dentro del volumen de medición.
- El “Juicio de Expertos”, que inicialmente iba a ser recogido en la ISO/TS 15530-5, pero que se abandonó al estar ya recogido en la Guía para la Expresión de la Incertidumbre de Medida (GUM) (18). El procedimiento usa los datos experimentales como base para una estimación tipo B de la incertidumbre de tareas de medición similares.
Uno de los problemas a los que hay que hacer frente es la disponibilidad de patrones con suficiente precisión, estabilidad, coste razonable y pequeña incertidumbres de calibración (19). Por otro lado, para poder trabajar en las escalas micro- y nano-, se desarrollaron unas CMMs capaces de proporcionar medidas que van desde los pocos micrómetros hasta el milímetro. Estas se conocen como micro-CMMs (20; 21) La verificación y calibración de las micro-CMM es de especial interés por la necesidad de obtener medidas 3D con gran precisión e incertidumbres bajas (22). Uno de los problemas que nos podemos encontrar es el propio palpado físico de las muestras. Las superficies de algunos materiales con dureza inferior a la de la punta del palpador empleado, o materiales depositados por técnicas como el sputtering, pueden verse dañados o destruidos por la interacción con la punta. Por ello, los instrumentos de medida ópticos 3D están ganando peso en el campo de la CM (23).
1.2. Microscopio confocal
Uno de los instrumentos de medida ópticos 3D más extendidos es el microscopio confocal. De acuerdo con la norma ISO 25178-6:2010, la microscopía confocal es “un método de medida de topografía superficial mediante el cual se captura la imagen de un objeto iluminado por una fuente de luz que pasa por un orificio estrecho. La luz es dirigida por unas lentes hacia la superficie que se está estudiando, donde se refleja y regresa a través de otra lente hacia un segundo orificio colocado frente a un detector. Este orificio funciona como un filtro que permite el paso al detector de la luz reflejada procedente de los puntos de la muestra situados en el plano focal” (24).
En la Figura 1 se muestra un esquema de un microscopio confocal.
Por el contrario, la luz procedente de planos superiores e inferiores al plano focal será rechazada por el material opaco que rodea al orificio (24; 26), tal como se puede ver en la Figura 2:
El detector captura la posición de todos los puntos que están en el plano focal. A medida que se enfoca en otros planos mediante el controlador que actúa sobre el eje Z, y se capturan los puntos correspondientes a otros planos focales, el software apila de manera organizada todas estas secciones digitalizadas, creando la reconstrucción tridimensional de la muestra analizada. Esta reconstrucción transforma los píxeles de cada imagen en vóxeles, cambiando la información de dos dimensiones a tres dimensiones, mediante una interpolación entre planos focales.
1.3. Equipo de medida
El equipo de medida que utilizamos en este trabajo podemos decir que tiene dos componentes:
- Unidad óptica: donde se incluyen los objetivos y todo el sistema de iluminación y detección.
- Unidad mecánica: que incluye una mesa de trabajo y la columna.
Las características del equipo son las siguientes (25):
- Microscopio confocal Leica DCM3D (Wetzlar, Germany) con un objetivo de 10× (EPI-L, NA = 0,30). El campo de visión es de 1270 μm × 952 μm [(768 × 576) píxeles]; con una anchura nominal de vóxel de 1.65 μm. El campo de trabajo total a lo largo del eje Z es de 944 μm, aunque el campo de trabajo típico para analizar la superficie de una muestra es de (100÷150) μm. Se usa un salto axial (altura de vóxel) de 2 μm.
- Software SensoSCAN—LeicaSCAN DCM3D 3.41.0 desarrollado por Sensofar Tech Ltd. (Terrassa).
- La unidad mecánica incluye una mesa de trabajo PRIOR (que permite desplazamientos de 150 mm en el eje X y 100 mm en el eje Y) y la “columna” (con una longitud de trabajo de 40 mm a lo largo del eje Z). En ambos casos, la resolución es de 0.1 μm y el movimiento se controla a través de un joystick.
El equipo está colocado sobre una mesa de granito para evitar posibles vibraciones externas. La habitación donde se encuentra el equipo está climatizada y, por tanto, se pueden controlar las condiciones ambientales de medida. Con estos elementos se pueden extraer medidas de dos formas diferentes que llamamos:
- “Modo microscopio”. Este modo de funcionamiento es el que se usa cuando la zona de medición es lo suficientemente pequeña como para que la muestra permanezca estática. Lo ideal en este modo de funcionamiento es trabajar en la parte central de la mesa de trabajo. Este modo de funcionamiento también permite obtener medidas del parámetro Ra de rugosidad.
- “Modo proyector de perfiles”, que es el que nos permite captar los desplazamientos de la unidad mecánica.
La combinación de ambos modos de funcionamiento (que llamaremos “modo combinado”) nos permite obtener medidas dimensionales 3D sobre muestras con un tamaño mayor que en otros microscopios de medida.
1.4. Objetivo del trabajo
En este trabajo se resumen los resultados obtenidos en:
- La Tesis Doctoral “Traceability of 3D optical measuring instruments in industrial environments using customized material standards” (27). En ella se exponen los resultados de la calibración del microscopio confocal cuando funciona en “modo combinado”.
- El artículo “Industrial Calibration Procedure for Confocal Microscopes” (25). En él se exponen los resultados de la calibración del microscopio confocal cuando funciona en “modo microscopio”. Como resultado adicional, se dota de trazabilidad a las medidas del parámetro Ra de rugosidad.
- El artículo “Design of Industrial Standards for the Calibration of Optical Microscopes” (1). En él se expone el problema que hay para encontrar patrones de referencia para medidas dimensionales a escalas micro- y nano- y se propone un procedimiento para fabricar patrones a medida utilizando tecnología láser.
Para más detalles sobre lo expuesto a continuación, recomendamos consultar dichos documentos.
2. METODOLOGÍA
De acuerdo con (27), la calibración de un instrumento de medida debe hacerse bajo las mejores condiciones disponibles. Las características metrológicas del instrumento de medida se deben estimar:
- Dentro del volumen de medición definido para el uso que se le vaya a dar. En este caso, el microscopio confocal se utiliza para hacer un análisis cuantitativo y cualitativo de superficies.
- Según un esquema de medida aceptado o acordado.
- En diferentes posiciones dentro del volumen de medición, en diferentes direcciones y velocidades de escaneo, si se puede. En este caso se van a utilizar unos patrones pensados para cubrir al máximo el volumen de medición.
El procedimiento de calibración completo incluye lo siguiente:
- Estimación de la desviación de planitud del plano focal utilizando un plano óptico.
- Calibración de las escalas de los ejes X e Y.
- Estimación del error de perpendicularidad entre los ejes X e Y.
- Calibración de la escala Z.
- Calibración del microscopio confocal para la medición de la rugosidad 2D utilizando patrones de rugosidad 2D periódicos.
- Todas las incertidumbres se estiman siguiendo el método descrito en la GUM (18) o en el documento EA-04/02 M:2013 (28), ya que son procedimientos estándar en laboratorios de calibración acreditados bajo ISO 17025 (29).
Dado que este procedimiento está pensado para ser utilizado en entornos industriales, el material de referencia elegido debe ser:
- Común en el campo de la metrología dimensional y la industria, para facilitar su adquisición, calibración y uso correcto.
- Fácil de encontrar o fabricar económicamente.
- Dimensionalmente estables y que garanticen largos intervalos de recalibración.
- Fácil de calibrar, con incertidumbres lo suficientemente bajas, en los Institutos Nacionales de Metrología (INM) o preferiblemente en laboratorios de calibración acreditados (ACL).
La calibración del sistema de medida completo tiene, por tanto, dos pasos:
- Calibración del microscopio confocal funcionando en “modo microscopio”.
- Calibración del microscopio confocal funcionando en “modo proyector de perfiles”.
Cada paso cuenta con los subpasos detallados a continuación.
2.1. Verificación de planitud
Antes de calibrar los ejes X e Y se debe realizar una verificación de la planitud del plano Z=0 (plano XY) del microscopio confocal. Los microscopios confocales introducen una ligera curvatura en el plano XY que se evidencia cuando se explora un patrón de planitud de vidrio (Figura 4a y Figura 5a). El defecto de planitud de estos patrones suele ser, de acuerdo con los fabricantes, de \(\frac{\lambda}{4}\left ( \sim 150 \ nm \right )\), \(\frac{\lambda}{10}\left ( \sim 60 \ nm \right )\) o \(\frac{\lambda}{20}\left ( \sim 30 \ nm \right )\) (28). En estos casos, esa superficie que es realmente plana se observa en el microscopio como una superficie curvada, como si fuera un casquete de una esfera o de un elipsoide. El instrumento permite corregir, mediante software, el posible defecto de planitud que presente el plano XY. Si esta operación se ha realizado correctamente, únicamente quedará un defecto de planitud residual que es el que se va a verificar.
Cuando el microscopio confocal funciona en “modo microscopio”, el procedimiento de calibración es el que se resume en la Figura 4b:
| a | b |
Cuando el microscopio confocal funciona en “modo proyector de perfiles”, el procedimiento de calibración es el que se resume en la Figura 5b:
| a | b |
Dado que el software nos proporciona el error cuadrático medio (RMS), lo vamos a utilizar. Hay que tener en cuenta que este parámetro, de acuerdo con (25; 29), es más estable estadísticamente.
2.2. Calibración del Plano XY
Para cuando el microscopio confocal funciona en “modo microscopio”, tanto en (30) como en (31) se propone el uso de una Regla Patrón de Trazos (RPT) (Figura 6a) para la calibración de los ejes X e Y en el caso de microscopios que funcionan con iluminación por reflexión. En (32; 33) se propone un procedimiento basado en (30) en el que se utiliza una RPT, dado que esta se puede calibrar fácilmente en un Instituto Nacional de Metrología o en un Laboratorio de Calibración Acreditado, colocada en diferentes posiciones (Figura 6b).
| a | b |
Para cuando el microscopio confocal funciona en “modo proyector de perfiles”, la primera idea sería utilizar una RPT más larga y medirla en diferentes posiciones a lo largo del eje X y a lo largo del eje Y. Sin embargo, habría que colocarla a mano y, por tanto, esto incrementaría mucho la incertidumbre. Por ello, tal y como se propone en (1), se fabrica un patrón a medida utilizando tecnología láser (Patrón XY, en la Figura 7a). El modelo que se grabó sobre una oblea de silicio monocristalino es el mostrado en la Figura 7b:
| a | b |
Este patrón de medida está pensado para esta aplicación concreta, pero el procedimiento de fabricación de este permitiría dotar de trazabilidad a las medidas hechas con los dos modos de funcionamiento y, además, se podría dotar de trazabilidad a otros objetivos.
Como se puede ver, este patrón tiene:
- Unas cruces centrales que están pensadas para dotar de trazabilidad a las mediciones hechas con la mesa de trabajo, por tanto, funcionando en “modo proyector de perfiles”.
- Unas mallas con distinto paso entre los trazos y en dos posiciones (a 0º y a 45º), para dotar de trazabilidad a las mediciones hechas con los objetivos, por tanto, funcionando en “modo microscopio”. Sería algo análogo a lo descrito en la Figura 6b.
En este trabajo se utilizarán únicamente las cruces centrales, puesto que en (25) se obtienen resultados de la incertidumbre para el “modo microscopio” de funcionamiento bastante buenos. Para poder quitar la histéresis del patrón, se realiza la medición girando el Patrón XY a 90º, 180º y 270º.
Tanto la RPT como el Patrón XY se han calibrado en el Laboratorio de Metrología y Metrotecnia (LMM) de la ETSII-UPM (acreditado por ENAC), utilizando un procedimiento específico para ello. El resultado de la calibración es el “paso medio” del patrón y la “distancia” entre las cruces, respectivamente. Se entiende por paso la distancia pi entre dos marcas o trazos sucesivos (i e i-1). El LMM certifica el valor medio l de todos los pi.
2.3. Calibración del eje Z
Se propone el uso de una esfera de referencia cuyo diámetro D0 puede ser obtenido mediante calibración en una Máquina Medidora de una Coordenada Horizontal (M1CH), de forma parecida a la que se lleva a cabo en (36). Dicha esfera de referencia puede ser una simple bola de rodamiento o una esfera de precisión (Figura 9a). Éstas poseen un defecto de esfericidad lo suficientemente bajo como para ser utilizadas como patrón de diámetro. Lo que sí es recomendable a la luz de la experiencia recogida en este trabajo es que la esfera elegida sea opaca. Previamente se intentó utilizar esferas de rubí de palpadores de MMCs (fácilmente disponibles en laboratorios de metrología dimensional), pero son muy difíciles de medir en un microscopio confocal debido a que son semitransparentes. La esfera se fija a un vidrio de microscopio (Patrón Z).
En este análisis se va a reconstruir el casquete esférico a partir de las coordenadas de los puntos de la superficie de esfera proporcionadas por el microscopio confocal. Tomando las medidas con el microscopio confocal y utilizando un software de cálculo (25), se reconstruye la superficie de la esfera y, así, se puede calcular el radio de esta y se puede estimar el parámetro de corrección que hay que aplicar para el caso en el que la esfera aparezca achatada o elongada a lo largo del eje Z (Figura 8). La calibración del eje Z mediante este procedimiento se tiene que llevar a cabo cando se haya calibrado el plano XY.
Cuando el microscopio confocal funciona en “modo microscopio”, el procedimiento de calibración es el que se resume en la Figura 9b:
| a | b |
Cuando el microscopio confocal funciona en “modo proyector de perfiles” hay que adaptar el procedimiento para incrementar la altura de forma controlada. Por ejemplo, en este trabajo se han utilizado Bloques Patrón Longitudinales (BPLs) de (5, 10, 15, 20 y 25) mm y se han colocado como se muestra en la Figura 10:
En cada altura se realiza una verificación de planitud para comprobar que, a lo largo del eje no hay ninguna desviación.
2.4. Calibración del parámetro de rugosidad Ra
La calibración en el eje Z garantiza la trazabilidad vertical de las mediciones hechas con el microscopio confocal. Como resultado adicional, se lleva a cabo una calibración de rugosidad, de acuerdo con los documentos (37; 38; 39), observando el parámetro Ra (proporcionado por el software) para cuando el microscopio confocal funciona en “modo microscopio”. Hay gran cantidad de parámetros que se utilizan para la caracterización de la textura de una superficie. Entre los parámetros 2D de amplitud de rugosidad, el más extendido es el Ra, que se corresponde con la media aritmética de los valores de las desviaciones respecto a la línea media del perfil de medida (40). De acuerdo con la norma ISO 4288 (41), para el rango de medida de 0,1 μm ≤ Ra ≤ 2 μm, la longitud de exploración es de 0,8 mm. Por otro lado, para Ra > 2 μm, la norma exige que la longitud de exploración sea mayor (2,5 mm o superior). Como el campo de medida del microscopio confocal es de (1270 x 952) μm, la calibración en rugosidad se va a llevar a cabo en el rango de 0,1 μm ≤ Ra ≤ 2 μm.
Los patrones utilizados para la medición de la rugosidad son los siguientes:
- Patrones de rugosidad periódicos irregulares metálicos (Figura 11a).
- Patrones de rugosidad periódicos regulares de vidrio (Figura 11b).
| a | b |
| c |
Los valores certificados de los patrones se pueden encontrar en (27).
3. RESULTADOS
El modelo matricial utilizado es el siguiente (27):
\(\begin{eqnarray} \begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix} 1+c_{xy,\ obj}+a_{obj} & \theta_{obj}/2 & 0 \\ \theta_{obj}/2 & 1+c_{xy,obj}-a_{obj} & 0 \\ 0 & 0 & 1+c_{z,obj} \\ \end{pmatrix} \cdot \nonumber\\ \begin{pmatrix} x_{obj} \\ y_{obj} \\ z_{obj}\end{pmatrix} +\begin{pmatrix} 1+c_{xy,\ wt}+a_{wt} & \theta_{wt}/2 & 0 \\ \theta_{wt}/2 & 1+c_{xy,\ wt} – a_{wt} & 0 \\ 0 & 0 & 1+c_{z,col} \\ \end{pmatrix} \cdot \begin{pmatrix} x_{s} \\ y_{s} \\ z_{s}\end{pmatrix} \end{eqnarray}\)
(1)
En la ecuación (1) se tiene en cuenta:
- Desviación relativa de la anchura del píxel respecto al nominal del objetivo \(\left(c_{xy,obj}\right)\) y del sistema \(\left(c_{xy,wt}\right)\).
- Diferencia relativa entre la anchura de los píxeles en el eje X y en el eje Y del objetivo \(\left(a_{objt}\right)\) y del sistema \(\left(a_{wt}\right)\).
- Error de perpendicularidad entre los ejes X e Y del objetivo \(\left(\theta_{obj}\right)\) y del sistema \(\left(\theta_{obj}\right)\).
- Corrección en el eje Z del objetivo \(\left(c_{z,obj}\right)\) y del sistema \(\left(c_{z,col}\right)\).
Para ver cómo calcular cada parámetro, consultar (25) y (27). Con él se pasa de tener el vóxel rojo, correspondiente a los datos brutos obtenidos del instrumento de medida, a tener el vóxel verde, que sería el corregido (Figura 12):
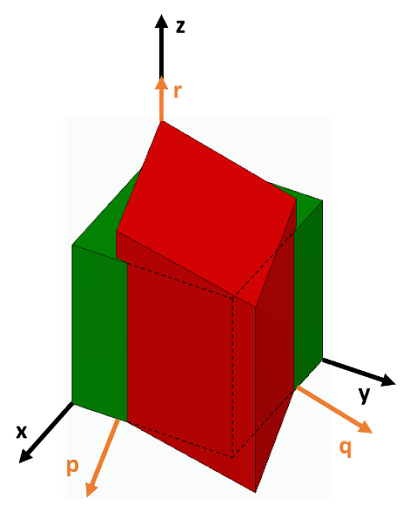
Propagando incertidumbres de acuerdo con la GUM, se obtuvieron las siguientes incertidumbres expandidas:
- Cuando el microscopio confocal funciona en “modo microscopio”:
- Mediciones punto a punto en el plano XY:
\(U\left ( L_{xy,obj} \right )\leq 1.9 ~ \mu m + \frac{L_{xy,obj}}{1600}\) (2) - Mediciones punto a punto en el eje Z:
\(U\left ( h_{obj} \right )\leq 2.2 ~ \mu m + \frac{h_{obj}}{120}\) (3)
- Mediciones de rugosidad:
\(U\left ( Ra \right )\leq 0.25 ~ \mu m\) (4)
- Mediciones punto a punto en el plano XY:
- Cuando el microscopio confocal funciona en “modo proyector de perfiles”:
- Mediciones punto a punto en el plano XY:
\(U\left ( L_{xy,vt} \right )\leq 7.8 ~\mu m + \frac{L_{xy,wt}}{3500}\) (5)
- Mediciones punto a punto en el eje Z:
\(U\left ( h_{col} \right )\leq 2.6 ~ \mu m + \frac{h_{col}}{133}\) (6)
- Mediciones punto a punto en el plano XY:
- Cuando el microscopio confocal funciona en “modo combinado”:
- Mediciones punto a punto en el plano XY:
\(U\left ( L \right )\leq 9.7 ~ \mu m + \frac{L}{1100}\) (7)
- Mediciones punto a punto en el eje Z: como las mediciones hechas con desplazamiento vertical de la columna incluyen las mediciones hechas por la unidad óptica, la ecuación (6) puede aplicarse al “modo combinado”.
- Mediciones punto a punto en el plano XY:
4. CONCLUSIONES
Se ha presentado un método de calibración completo que dota de trazabilidad adecuada a las escalas para las mediciones de longitud y de rugosidad realizadas con el sistema óptico de un microscopio confocal.
- El procedimiento de calibración es razonablemente simple.
- Se seleccionan patrones de referencia fáciles de encontrar y de calibrar.
- El procedimiento permite estimar:
- Para las mediciones dimensionales: coef. de amplificación, defectos de linealidad y planitud, errores de perpendicularidad, repetibilidad y la diferencia relativa entre las dimensiones del pixel en los ejes X e Y.
- Para las mediciones de rugosidad: el sesgo que aparece, la repetibilidad y el ruido del instrumento, que afecta a la medición de la rugosidad Ra.
- Se consigue una fórmula que da una solución al problema de estimar las incertidumbres para un número finito de tareas metrológicas.
En cuanto al modelo global de calibración:
- Permite realizar mediciones trazables dentro del volumen de medición del instrumento.
- Pone de manifiesto las grandes incertidumbres que puede llegar a introducir el movimiento de la mesa. Las incertidumbres introducidas por el movimiento de la mesa dependen directamente de la calidad de esta. Una buena mesa XY debería ser capaz de dar incertidumbres menores de 1 µm.
La metodología propuesta podría usarse para:
- Dotar de trazabilidad a otros instrumentos de medida similares, es decir, que trabajen con imágenes representadas por vóxeles (variación de foco y máquinas de visión).
- Dotar de trazabilidad a las medidas realizadas con instrumentos ópticos 3D en entornos industriales.
- Ofrecer servicios de calibración a la industria.
- Acreditar medidas dimensionales con instrumentación óptica 3D en laboratorios de calibración.
Por otro lado, la búsqueda de patrones sencillos y accesibles es compleja. Existen patrones comerciales muy completos y teóricamente muy interesantes pero muy caros y difíciles de obtener y calibrar. Se han determinado los parámetros del proceso y se ha diseñado y fabricado un patrón que permite dotar de trazabilidad a diferentes tareas de medición comunes en metrología, siguiendo en líneas generales la normativa vigente:
- Se pueden fabricar patrones pasa – no pasa 100 % configurables con geometrías complejas.
- El proceso de calibración del patrón es sencillo, aunque mejorable.
- A nivel industrial, se puede abrir una línea de trabajo para producir patrones calibrables.
- Usando láseres con menor ancho de pulso, se podría mejorar la calidad del patrón.
Referencias
1. Design of Industrial Standards for the Calibration of Optical Microscopes. Mínguez Martínez, A., et al. 29, 2021, Materials, Vol. 14 (1).
2. Madou, M.J. Scaling, Actuators, and Power in Miniaturized Systems. Fundamentals of Microfabrication, The Science of Miniaturization. 2nd edition. Boca Raton : CRC Press, 2002, pp. 407-448.
3. The miniaturization technologies: past, present, and future. Frazier, A.B., Warrington, R.O. and Friedrich, C. 5, s.l. : IEEE, 1995, IEEE Transactions on Industrial Electronics, Vol. 42, pp. 423 – 430.
4. The future of manufacturing industry: a strategic roadmap toward Industry 4.0. Morteza, Ghobakhloo. 6, s.l. : Emerald Publishing, 2018, Journal of Manufacturing Technology Management,, Vol. 29, pp. 910-936.
5. Smart factory in Industry 4.0. Shi, Z., et al. 4, s.l. : Wiley Online Library, 2020, System Research and Behavioral Science, Vol. 37, pp. 607-617.
6. A Review of AdditiveManufacturing. Wong, K.V. and Hernandez, A. Article ID 208760, 2012, ISRN Mechanical Engineering, Vol. 2012, p. 10.
7. Surface texture metrology for metal additive manufacturing: a review. Townsend, A., et al. 2016, Precision Engineering.
8. Sladek, J.A. Coordinate Metrology. Accuracy of Systems and Measurements. 1. Berlin : Springer, 2016. ISSN 2195-9862.
9. Joint Commitee for Guides in Metrology (JCGM). International Vocabulary of Metrology (VIM). 3. Paris : JCGM Publications, 2012.
10. International Organization for Standardization (ISO). 10360-1:2000 – Geometrical Product Specifications (GPS). Acceptance and reverification tests for coordinate measuring machines (CMM). Part 1: Vocabulary. Geneva : ISO Publications, 2000.
11. Leach, R.K. and Smith, S. Basics of Precision Engineering. s.l. : CRC Press, 2018. 9781351204118.
12. Leach, R.K. Fundamental Principles of Engineering Nanometrology. Kidlington : Elsevier, 2010. ISBN 978-0-08-096454-6.
13. Proposal for changes in the ISO 15530 series of standards. Płowucha, W. and Jakubiec, W. Cluj-Napoca, Romania : s.n., 2012. Vol. 13, pp. 237-240.
14. International Organization for Standardization (ISO). 15530-3:2004 (ISO/TS) – Geometrical product specifications (GPS). Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement. Part 3: Use of calibrated workpieces or standards. Geneva : ISO Publications, 2005.
15. —. 15530-4:2008 (ISO/TS) – Geometrical product specifications (GPS). Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement. Part 4: Evaluating task-specific measurement uncertainty using simulation . Geneva : ISO Pulbications, 2008.
16. —. 15530-2 (ISO/DTS) – Geometrical product specifications (GPS). Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement. Part 2: Use of multiple measurement strategies in measurements of artefacts. Geneva : ISO Publications.
17. Achieving Traceability of Industrial Computed Tomography. Bartscher, M., et al. s.l. : Trans Tech Publications, 2010, Key Engineering Materials, Vol. 437, pp. 79-83. 1662-9795.
18. Joint Committee for Guides in Metrology, Working Group 1 (JCGM/WG1). JCGM 100:2008 Evaluation of measurement data – Guide to the expression of uncertainty in measurement (GUM). Paris : JCGM Publications, 2008.
19. Savio, E., Hansen, H.N. and De Chiffre, L. Approaches to the Calibration of Freeform Artefacts on Coordinate Measuring Machines. CIRP Annals Manufacturing Technology. s.l. : ELSEVIER, 2002. Vol. 51, 1, pp. 433-436. 0007-8506.
20. Recent developments in dimensional metrology for microsystem components. Cao, S., et al. s.l. : Springer, 2002, Microsystem Technologies, Vol. 8, pp. 3-6.
21. Takaya, Y. and Michihata, M. Optical Micro-CMM. [book auth.] W. Gao. Metrology. Precision Manufacturing. Singapore : Springer, 2019.
22. A review of the existing performance verification infrastructure for micro-CMMs. Claverley, J.D. and Leach, R.K. s.l. : Elsevier, 2015, Precision Engineering, Vol. 39, pp. 1-15.
23. Traceable optical coordinate metrology applications for the micro range. Ehrig, W., et al. San Jose (CA-US) : SPIE, 2009. Proceedings Three-Dimensional Imaging Metrology. Vol. 7239. 72390G.
24. International Organization for Standardization (ISO). 25178-6:2010 – Geometrical Product Specifications (GPS). Surface texture: Areal. Part 6: Classification of methods for measuring surface texture. Geneva : ISO Publications, 2010.
25. Industrial Calibration Procedure for Confocal Microscopes. Mínguez Martínez, A. and de Vicente y Oliva, J. 4137, s.l. : MDPI, 2019, Materials, Vol. 12.
26. Giusca, C.L. and Leach, R.K. Measurement Good Practice Guide (No. 128): Calibration of the metrological characteristics of imaging confocal microscopes (ICMs). Teddington, Middlesex, United Kingdom : National Physical Laboratory, 2012.
27. Mínguez-Martínez, A. Traceability of 3D optical measuring instruments in industrial environments using customized material standards. Madrid, Spain : s.n., 2021. E.T.S.I. Industriales (UPM).
28. International Organization for Standardization (ISO). 25178-700 (ISO/DIS) – Geometrical product specifications (GPS). Surface texture: Areal. Part 700: Calibration, adjustment and verification of areal topography measuring instruments. Geneva : ISO Publications.
29. European Accreditation (EA). EA-4/02 M 2013 – Evaluation of the Uncertainty of Measurement in Calibration. s.l. : EA Publications, 2013.
30. International Organization for Standardization (ISO). 17025:2017 (ISO/IEC) – General requirements for the competence of testing and calibration. Geneva : ISO Publications, 2017.
31. EDMUND OPTICS. Optical Flats. Edmund Optics website. [Online] EDMUND OPTICS. [Cited: 02 24, 2022.] https://www.edmundoptics.es/knowledge-center/application-notes/optics/optical-flats/.
32. NIST/SEMATECH. e-Handbook of Statistical Methods. [Online] [Cited: 11 27, 2019.] http://www.itl.nist.gov/div898/handbook/.
33. CEM. Procedimiento DI-001 para la Calibración de Proyectores de Perfiles. Madrid : Ministerio de Industria, Energía y Turismo, 2013.
34. CEM. Procedimiento DI-006 para la Calibración de Microscopios de Medida. Madrid : Ministerio de Industria, Comercio y Turismo, 1999.
35. Calibración de Microscopios Confocales. de Vicente, J., et al. XVII Congreso Nacional de Ingeniería Mecánica. pp. 307-312.
36. Uncertainty Estimation for Performance Evaluation of a Confocal Microscope as Metrology Equipment. Guarneros, O., et al. 1, 2014, MAPAN – Journal of Metrology Society of India, Vol. 29, pp. 29-42.
37. Performance verification of a confocal microscope for 3D metrology tasks. Balcon, M., Carmignato, S. and Savio, E. 5, 2012, Quality – Access to Success, Vol. 13, pp. 63-66.
38. Deutscher Kalibrierdienst (DKD). Guideline DKD 4-2 Calibration of measuring instruments and standards for roughness measuring technique (Sheet 1: Calibration of standards for roughness measuring technique). Braunschweig (GERMANY) : DKD, 2009.
39. —. Guideline DKD-R 4-2 Calibration of Devices and Standards for Roughness Metrology (Sheet 2: Calibration of the vertical measuring system of stylus instrument). Braunschweig (GERMANY) : DKD, 2007.
40. —. Guideline DKD-R 4-2 Calibration of Devices and Standards for Roughness Metrology (Sheet 3: Calibration of standards with periodic profiles in horizontal direction by means of stylus instrument). Braunschweig (GERMANY) : DKD, 2011.
41. European Committee for Standardization (CEN). ISO 4287:1999 Geometrical Product Specifications (GPS) Surface texture: Profile method. Terms, definitions and surface texture parameters. Bruxelles : CEN, 1999.
42. —. ISO 4288:1996 Geometrical product specifications (GPS) Surface Texture: Profile method. Rules and procedures for the assessment of surface texture. Bruxelles : CEN, 1996.









Comentarios