José Juan Segovia Puras, Universidad de Valladolid
Dolores del Campo, Centro Español de Metrología


Resumen
El 20 de mayo de 2019 entró en vigor la revisión del Sistema Internacional de Unidades, SI, con el objetivo de vincular la definición de las unidades fundamentales con constantes físicas. La redefinición del kelvin está basada en la constante de Boltzmann. En este artículo se presenta un resumen de los trabajos realizados con los termómetros termodinámicos: termómetro de gas acústico, termómetro de constante dieléctrica de gases, termómetro de ruido Johnson y termómetro de ensanchamiento Doppler, que han conducido a que el Grupo de Constantes Fundamentales de CODATA fijara el valor numérico de la constante de Boltzmann en 1,380 649 03 (51) x 10-23 J K-1, con una incertidumbre de 3,7 x 10-7 J K-1. Este valor se trunca y redondea definiendo la constante del SI revisado como k = 1,380 649 x 10-23 J K-1, siendo el valor que se empleará para la nueva definición del kelvin y que no tiene incertidumbre.
Palabras clave
SI, Sistema Internacional de Unidades, kelvin, constante de Boltzmann, termómetro termodinámico.
Abstract
On May 20th, 2019, the revision of the International System of Units, SI, entered into force, with the aim of linking the definition of the fundamental units with physical constants. The redefinition of the kelvin is based on the Boltzmann constant. This paper presents a summary of the work done with thermodynamic thermometers: acoustic gas thermometer, dielectric constant gas thermometer, Johnson noise thermometer and Doppler widening thermometer, which have led to the CODATA Group of Fundamental Constants set the numerical value of the Boltzmann constant to 1,380 649 03 (51) x 10-23 J K-1, with an uncertainty of 3.7 x 10-7 J K-1. This value is truncated and rounded, defining the revised SI constant as k = 1,380 649 x 10-23 J K-1, which is the value used for the new definition of the kelvin that has no uncertainty.
Key words
SI, International System of Units, kelvin, Boltzmann constant, thermodynamic thermometer.
Introducción
El sistema internacional de unidades está basado en siete unidades fundamentales, donde la definición de una unidad se basa en una cantidad invariante de la física.
El Comité Internacional de Pesas y Medidas (CIPM) recomendó en octubre de 2005, [1], durante su 94ª reunión, iniciar la preparación de una nueva definición de cuatro de las unidades fundamentales, kilogramo, amperio, kelvin y mol, que las vinculase con cuatro constantes físicas, de valores exactamente definidos, la constante de Planck h, carga elemental e, constante de Boltzmann k y constante de Avogadro NA.
En octubre de 2011, la 24ª reunión de la Convención General de Pesas y Medidas (CGPM), [2], en la primera resolución, consideró que era posible redefinir el kelvin a partir de un valor numérico exacto de la constante de Boltzmann k.
Detrás de cada una de estas constantes hay una teoría fundamental de la física, para la constante de Boltzmann son la mecánica estadística y la termodinámica.
La constante de Boltzmann es el puente entre la energía térmica y la energía mecánica ligando las unidades J y N·m que representan la misma magnitud: energía.
Como la energía térmica microscópica kT no es directamente accesible mediante un experimento, las cantidades macroscópicas, que están correlacionadas inequívocamente con la energía térmica [3], deben medirse para la determinación de k a una temperatura conocida. Esta temperatura es la del punto triple del agua ya que era el punto que se había utilizado hasta el momento para la definición del kelvin. Los termómetros termodinámicos son los únicos instrumentos que pueden establecer directamente esta relación.
Estos termómetros establecen una relación entre el mensurando y la temperatura termodinámica, que no contiene constantes desconocidas dependientes de la temperatura, permitiendo el cálculo de la incertidumbre, con la máxima exactitud posible.
Los termómetros termodinámicos necesarios para realizar medidas de la constante de Boltzmann están suficientemente detallados en la bibliografía, en abierto, para su difusión en la comunidad científica, y los laboratorios han podido realizar sus medidas de forma independiente.
La nueva definición del kelvin en términos de la constante de Boltzmann ha requerido de un gran esfuerzo experimental; solo la combinación de varios resultados independientes, obtenidos con diferentes métodos y en diferentes laboratorios, han podido hacer posible esta nueva definición. Este esfuerzo investigador se canalizó a través del proyecto europeo auspiciado por EURAMET “Determination of the Boltzmann constant for the redefinition of the kelvin” , financiado parcialmente por la Unión Europea, con la participación de los Institutos Nacionales de Metrología, CEM (España), DFM (Dinamarca), INRIM (Italia), LNE-CNAM (Francia), NPL (Reino Unido) y PTB (Alemania). También participaron varias universidades europeas: Seconda Universitá degli Studi di Napoli (Italia), Politecnico di Milano (Italia), Université Sorbonne Paris Nord (Francia) y la Universidad de Valladolid (España, UVa).
En junio de 2014, el CCT recomendó que el Grupo de Constantes Fundamentales de CODATA fijara el valor numérico de la constante de Boltzmann bajo dos premisas:
• La incertidumbre estándar relativa en el ajuste de k debe ser menor que 1 × 10−6.
• La determinación de k debe de estar basada en al menos dos métodos fundamentales diferentes, donde al menos un resultado de cada uno tenga una incertidumbre estándar relativa menor de 3 × 10−6.
Las técnicas experimentales que han conseguido cumplir estos requisitos, y que se comentan en los siguientes párrafos han sido: el termómetro de gas acústico, termómetro de constante dieléctrica de gases y el termómetro de ruido Johnson.
En 2017, el Comité Internacional de Pesas y Medidas (CIPM) [4] y la Conferencia General de Pesas y Medidas (CGPM) [5] solicitaron al Comité de Datos para la Ciencia y la Tecnología (CODATA) un ajuste especial [6] para determinar los valores recomendados de las constantes físicas para la revisión del Sistema Internacional de Unidades (SI) en 2018 [7], [8], entrando en vigor en 2019 [9].
Termómetro de gas acústico, AGT.
La velocidad del sonido u en un gas real viene dada como función de la densidad ρ:
\(u^2=(\frac{\partial p}{\partial\rho})_S=A_0\ (1+\beta_a\ \rho_n+\gamma_a\ \rho_n^2+\ldots)\)
donde βa, γa son los coeficientes del virial acústicos y A0 la velocidad del sonido a densidad cero
\(A_0=\frac{kN_A\ T\gamma^pg}{M}\)
k es la constante de Boltzmann, NAel número de Avogadro, T la temperatura termodinámica, γpg es el coeficiente adiabático como gas ideal y M la masa molecular. Para obtener incertidumbres relativas del orden de 10-6, todas las variables tienen que tener incertidumbres de este orden. Los valores teóricos de las propiedades termofísicas de gases monoatómicos como helio y argón se calculan a partir de los fundamentos de la mecánica cuántica y la mecánica estadística.
En un resonador esférico las frecuencias acústicas de resonancia de un gas se expresan en función de la velocidad del sonido con la siguiente expresión:
\(f_N^a=\frac{u}{2\pi a_0}\times\frac{a_0}{a}\nu_N^a+\Delta f_N^a\)
donde a es el radio a presión p, a0 el radio a presión cero, νNa es un eigenvalor conocido exactamente, y ΔfNa la suma de los términos de corrección (N denota el modo de resonancia).
La corrección más importante es debida a la capa límite térmica cerca de la pared del resonador, otras contribuciones al término de corrección tienen en cuenta el acoplamiento entre el gas y la pared que se evalúa a partir de las constantes elásticas del material. La última de las correcciones tiene en cuente la presencia de orificios.
Para determinar la velocidad del sonido u requerimos de una determinación independiente del radio. Existen varias posibilidades, la primera es utilizar un fluido patrón con velocidades del sonido conocidas. Este método, siendo el más sencillo, conduce a las mayores incertidumbres. Otra posibilidad es utilizar técnicas picnométricas empleando mercurio como fluido de trabajo, este procedimiento fue seguido por Moldover en su trabajo para la determinación de R [10]. En este caso tenemos un problema de contaminación y un aumento de la incertidumbre para volúmenes pequeños.
La tercera posibilidad, que conduce a la menor incertidumbre, es determinar las frecuencias de resonancia medias de los modos degenerados en el campo de las microondas. En el vacío tenemos la siguiente expresión:
\(\frac{c}{a_0(T)}=\frac{2\pi\left\langle f’_m(T)\right\rangle}{z_m}\)
Donde \(\left\langle f’_m\right\rangle\) son las frecuencias medias corregidas de microondas, zm una constante numérica conocida y c la velocidad de la luz en el vacío.
La expansión térmica de la cavidad se determina a partir de medidas de las resonancias en el campo de las microondas. El volumen de la cavidad se obtiene a partir de las medidas de las frecuencias de los multipletes degenerados, ya que sus frecuencias medias se pueden determinar con un alto grado de exactitud. La parte real u e imaginaria v de la señal trasmitida por el resonador se ajusta a una suma de funciones complejas de la frecuencia:
\(u+iv=\sum_{m=0,\pm1}\frac{2ifg_mA_{1n}^{m}}{F_{1n}^{m_{2}}-f^2}+B+C(F_{1n}^{m}-f)\)
donde A, B y C son constantes complejas y FN= fN + i gN son las frecuencias de resonancia complejas degeneradas de los modos estudiados.
Los trabajos para la determinación la constante de Boltzmann k, con resonadores acústicos esféricos, se realizaron en los laboratorios del INRiM, LNE-CNAM, NPL y de la UVa en colaboración con el CEM. Debido a su experiencia, el instituto nacional de EEUU, NIST, colaboró con todos estos experimentos y, además, el instituto nacional chino NIM también realizó medidas empleando un resonador cilíndrico. Esta colaboración proporcionó resultados redundantes tanto por el número de laboratorios como por las diferentes técnicas.
Los resonadores esféricos tienen una geometría elipsoidal triaxial, y su construcción varía según el tamaño y los materiales. Una de las ventajas de la técnica es la determinación “in situ” de las dimensiones de la cavidad con la mínima incertidumbre. Cada laboratorio ha aplicado las correcciones con modelos que dependen de la frecuencia de resonancia, las dimensiones y materiales del resonador y del gas empleado, lo que posibilita la redundancia en el análisis de los resultados.
El resonador CEM-UVa está construido en acero inoxidable recubierto con una película de oro de 15 μm en su superficie interior, para conseguir una alta conductividad eléctrica y sin material oxidante. El radio es de 4 cm lo que conduce a un volumen de 0,25 dm3.

Los transductores acústicos son de tipo capacitivo y el gas empleado ha sido argón, la incertidumbre estándar relativa conseguida es 6,7 × 10−6 [11].
El INRiM ha diseñado un resonador desalineado, construido a partir de dos semiesferas perfectas de 9 cm de radio, el material empleado ha sido cobre, lo que mejora la conductividad eléctrica. Los experimentos se han llevado a cabo con helio, que presenta la ventaja de poder calcular las propiedades termofísicas con la mínima incertidumbre, por el contrario, es muy sensible a las impurezas por la presencia de otros compuestos o isótopos. La mejor incertidumbre relativa estándar encontrada es 1,06 × 10−6 [12].
El LNE-CNAM ha conseguido la mínima incertidumbre en la determinación de k. Esto ha sido posible gracias a un resonador cuasiesférico de 3 l, con 9 cm de radio. El resonador es un elipsoide triaxial de cobre con un acabado superficial realizado con herramienta de punta de diamante. Junto con la calidad de la cuasiesfera, el punto más importante para conseguir la menor incertidumbre ha sido emplear helio, purificado “in situ” y con la composición isotópica conocida por espectroscopía de masas. La mejor incertidumbre relativa estándar encontrada es 0,56 × 10−6 [13].
El NPL ha construido también una cuasiesfera, con un gran acabado superficial, formada por dos semiesferas de cobre que forman un elipsoide triaxial de 6,2 cm de radio. Como gas se empleó argón, que impidió conseguir una menor incertidumbre debido al impacto de las impurezas y la composición isotópica. En 2017 se revisó el valor aportado con una incertidumbre relativa estándar de 0,70 × 10−6 [14].
El NIM es el único laboratorio que empleó un resonador cilíndrico, con un diámetro de 8 cm y construido en cobre OFHC, la longitud de la cavidad se determina por interferometría óptica. Debido a la diferente geometría el espectro de resonancias acústicas es muy diferente al de esferas. El gas empleado fue argón. Este trabajo se realizó en colaboración con el NIST y supone una prueba de la teoría en busca de efectos sistemáticos. La mejor incertidumbre relativa estándar encontrada es 2,0 × 10−6 [15].
Termómetro de constante dieléctrica de gases, DCGT.
El principio de medida se basa en reemplazar la densidad en la ecuación de estado de un gas por la constante dieléctrica y medirla mediante los cambios de capacitancia de un condensador, lleno con el gas, en función de la presión. La técnica se basa en la medida de la variación relativa de la capacidad de un condensador cilíndrico lleno de gas respecto a otro en vacío (ε – ε0) a diferentes presiones p y a la temperatura del punto triple del agua. Los datos se ajustan a una expansión del virial a partir del primer término (lineal) A1 que describe el comportamiento ideal del gas:
\(A_1=\left(\frac{A_\varepsilon}{RT}+\frac{\kappa_{eff}}{3}\right)^{-1}\)
Donde Aε es la polarizabilidad molar y κeff es la compresibilidad efectiva del condensador, que se calcula a partir de las propiedades elásticas del material con el que está fabricado. El valor k se deduce de la relación Aε/R como:
\(k=\frac{\alpha_0}{3\varepsilon_0}/\frac{A_\varepsilon}{R}\)
Donde ε0 es una constante eléctrica fija y la polarizabilidad atómica es α0 = 2,281 513 31·10-41 C·m2·V-1, calculada ab initio con una incertidumbre estándar relativa de 0,1 × 10−6.
El diseño del condensador cilíndrico de medida y el material de construcción son etapas críticas. El material empleado para los electrodos es carburo de tungsteno, que tiene una compresibilidad que es aproximadamente el doble del acero inoxidable. Esto ha permitido la reducción de la componente de incertidumbre debida a la compresibilidad efectiva κeff, por el cambio de la capacitancia como consecuencia de la deformación y el desplazamiento relativo de los electrodos del condensador bajo presión.
La capacidad de un condensador ideal de geometría cilíndrica viene dada por:
\(C_{cilindro}=\frac{2\pi\varepsilon l}{ln\frac{d_0}{d_i}}\)
Donde ε es la constante dieléctrica, l la longitud del electrodo, d0 el diámetro interno del electrodo externo y di el diámetro externo del electrodo interno.
Para detectar cambios de capacitancia se midieron presiones hasta 7 MPa con una incertidumbre estándar relativa de 1,0 × 10−6. Con este fin, se diseñó, construyó y evaluó un sistema de balanzas de presión que mejoró la incertidumbre del patrón nacional de presión del PTB. Las experiencias se han realizado con helio de alta pureza. Tras las sucesivas mejoras, se ha conseguido reducir la incertidumbre relativa estándar a 1,94 × 10−6 [16].
Termómetro de ruido Johnson, JNT.
Los termómetros de ruido Johnson se basan en la medida del ruido de voltaje (o corriente) fluctuante que aparece en un conductor eléctrico, donde el sensor es una resistencia, debido al movimiento térmico de los electrones en el conductor. La ley de Nyquist describe el voltaje para temperaturas de 300 K y frecuencias inferiores a 10 MHz con una incertidumbre menor que 1,0 × 10−9:
\(\left\langle V_T^2\right\rangle=4kTR_{el}\Delta f\)
donde VT es el voltaje RMS del ruido de Johnson, Rel es la resistencia del resistor, y Δf es el ancho de banda para la medida del ruido. k se puede determinar a partir de las fluctuaciones del voltaje a la temperatura del punto triple del agua en el resistor. El ruido del voltaje es bajo y aleatorio (~1,2 nV·√Hz‑1), y debe ser medido para anchos de banda grandes y largos periodos de tiempo, lo que dificulta la determinación práctica de k con suficiente precisión.
El hito más importante en el desarrollo del termómetro ha sido la construcción, por el NIST, de una fuente de tensión de ruido de precisión cuántica QVNS que permite la calibración de la respuesta de ganancia y frecuencia del termómetro de ruido de Johnson. La fuente QVNS iguala las potencias de ruido de las dos fuentes para eliminar los efectos no lineales, a su vez, el igualar las impedancias de las dos fuentes de ruido produce un aumento significativo del ancho de banda. Esta mejora ha permitido medir de una forma práctica la temperatura.
La amplitud del voltaje de ruido térmico y el voltaje QVNS se pueden trazar al efecto Hall cuántico y al efecto Josephson, y la fuente de ruido térmico se mantiene en el punto triple del agua, lo que permite determinar la relación k / h, donde h es la constante de Planck con incertidumbre no significativa al ser mucho menor que la de k, de acuerdo a los valores recomendados por CODATA.
Los resultados preliminares del NIST conducen a una incertidumbre estándar relativa de 12,1 × 10−6, tras la colaboración del NIST y el NIM en 2015 para el desarrollo de un nuevo JNT-QVNS en el NIM se ha conseguido reducir la incertidumbre relativa estándar a 3,9 × 10−6 [17].
En 2017 el NIST realizó mejoras en el equipo, como aumentar el valor de la resistencia de 100 Ω a 200 Ω y la nueva determinación consigue reducir la incertidumbre a 5,0 × 10−6 [17]. El NIM realizó también en 2017 nuevas determinaciones encontrando una incertidumbre relativa estándar de 2,7 × 10−6 [18], cumpliendo con los requerimientos del CCT.
Termómetro de ensanchamiento Doppler DBT.
La implementación de los termómetros de ensanchamiento Doppler se basa en el perfil ampliado Doppler exhibido en la línea de absorción molecular de un gas en equilibrio termodinámico, relacionado con la distribución de velocidad de Maxwell-Boltzmann de las partículas del gas. A continuación, se obtiene k a partir de la anchura “e-fold half-Doppler” ΔνD como:
\(k=\frac{mc^2}{2T}\left(\frac{\Delta\nu_D}{\nu_0}\right)^2\)
donde ν0 es la frecuencia central de la línea, c es la velocidad de la luz de la espectroscopia láser utilizada, y m es la masa molecular.
Para extraer el componente Doppler del ancho de la línea de absorción, la forma de la línea se ajusta a un modelo físico cuya selección es crucial. Para el caso de una sola línea molecular roto-vibratoria a bajas presiones, el ensanchamiento Doppler es un perfil gaussiano. Pero las colisiones moleculares inducen una forma de línea general siguiendo un perfil de Voigt, convolución del Gaussiano con un perfil Lorentziano. Si se tienen en cuenta los efectos de estrechamiento dependientes de la velocidad y de Lamb-Dicke-Mössbauer, la suposición de colisiones moleculares duras o blandas da lugar a diferentes perfiles de Voigt.
La Université Paris Nord en colaboración con el LNE-CNAM consiguieron como mejor incertidumbre relativa estándar 24 × 10−6, sus investigaciones han continuado y han demostrado que, en teoría, es posible conseguir incertidumbres de 2,3 × 10−6 con termometría DBT en amoniaco [19].
La Seconda Università degli Studi di Napoli en colaboración con el Politecnico di Milano y el INRiM han realizado la determinación de k empleando espectroscopía de absorción por medio de dos láseres operando a la frecuencia de 1,39 μm. El método consiste en la determinación de la línea 44,1 → 44,0 de la banda H218O n1 + n3, en una muestra de vapor de agua en equilibrio termodinámico. El último resultado encontrado ha conseguido reducir la incertidumbre relativa estándar a 24 × 10−6 [20].
Ajuste de constantes fundamentales, datos y análisis para el CODATA 2017
Los trabajos realizados en el proyecto europeo para la determinación de la constante de Boltzmann, 2008-2011, fueron el punto de partida para una nueva definición del kelvin, y que posteriormente han contado con la colaboración de Institutos Nacionales de Metrología del resto del mundo. Las cuatro técnicas descritas han contribuido a la nueva determinación de la constante de Boltzmann realizada por CODATA [8], aunque la termometría DBT tiene incertidumbres altas que no cumplen con el criterio de aceptación del CCT.
CODATA realizó un ajuste multivariable por mínimos cuadrados de todos los datos existentes identificando los casos donde el coeficiente de sensibilidad es menor del 1%, estos valores se eliminan del ajuste final al no ser significativos para el valor final ajustado.
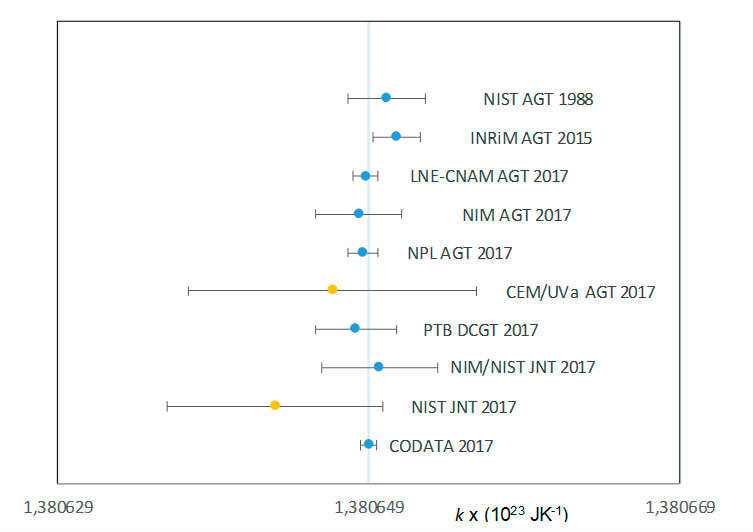
Los mejores resultados encontrados, y que han sido la base, para el ajuste especial de la constante de Boltzmann llevado a cabo por el comité de Datos para la ciencia y la Tecnología (CODATA) en 2007 se presentan en la tabla 1 y en la figura 3.
| Instituto | Termómetro | k (k x 1023 J K-1) | Gas | Incertidumbre (u x 106) | Año |
| NIST [38] | AGT | 1,380 6502 | Ar | 1,8 | 1988 |
| INRiM [25] | AGT | 1,380 6508 | He | 1,1 | 2015 |
| LNE-CNAM [26] | AGT | 1,380 648 80 | He | 0,6 | 2017 |
| NIM [27] | AGT | 1,380 6484 | Ar | 2,0 | 2017 |
| NPL [46] | AGT | 1,380 648 62 | Ar | 0,7 | 2017 |
| CEM/UVa [29] | AGT | 1,380 6467 | Ar | 6,7 | 2017 |
| PTB [52] | DCGT | 1,380 6482 | He | 1,9 | 2017 |
| NIM/NIST [85] | JNT | 1,380 6497 | 2,7 | 2017 | |
| NIST [87] | JNT | 1,380 6430 | 5,0 | 2017 |
Tabla 1. Mejores determinaciones de k realizadas por los Centros Nacionales de Metrología con los diferentes métodos, que contribuyen a la reevaluación del SI realizada por CODATA.
El valor final de CODATA [6] para k es 1,38064903 (51) x 10-23 J K-1 [3,7 x 10-7]. Este valor se trunca y redondea definiendo la constante del SI revisado k = 1,380649 x 10-23 J K-1, siendo el valor que se empleará para la definición del kelvin y que no tiene incertidumbre. Este valor fue aprobado en la 106ª reunión del CIPM, el Comité Consultivo de Temperatura recomendó ocho dígitos significativos para k, sin embargo, el octavo dígito es cero, por lo que solo se requieren siete.
Conclusiones
La determinación de la constante de Boltzmann para la nueva definición del kelvin ha sido un esfuerzo internacional que comenzó con el proyecto EURAMET financiado parcialmente por la Unión Europea, con la participación de los principales Centros Nacionales de Metrología de Europa y la colaboración del NIST y el NIM.
Esta colaboración ha continuado en el tiempo, más allá del límite del proyecto, hasta el año 2017, cuando se publican los mejores resultados, aprobados por CODATA.
La termometría acústica AGT es la técnica más desarrollada con incertidumbres por debajo de 1,0 x 10-6, los termómetros de constante dieléctrica DGCT y de ruido Johnson JNT también han conseguido incertidumbres estándar relativas menores de 3 × 10−6, cumpliendo las recomendaciones del Grupo de Constantes Fundamentales de CODATA.
El valor numérico asignado a la constante de Boltzmann es k = 1,380649 x 10-23 J K-1, sin incertidumbre y es la referencia para la definición del kelvin. La temperatura termodinámica ya no necesitará de un punto fijo para su realización y las futuras mejoras en las medidas no afectarán a la definición.
Bibliografía.
[1] Mills I, Mohr PJ, Quinn TJ, Taylor BN and Williams ER. 2006. Redefinition of the kilogram, ampere, kelvin and mole: a proposed approach to implementing CIPM recommendation 1 (CI-2005). Metrologia 43:227–246.
[2] http://www.bipm.org/en/si/new_si/
[3] Fellmuth B, Gaiser C, Fischer J. 2006. Determination of the Boltzmann constant—status and prospects. Meas Sci Technol. 17:R145–59.
[4] International Committee for Weights and Measures. 2017. “Proceedings of the 106th meeting,” Sèvres.
[5] General Conference on Weights and Measures. 2018. “Draft Resolution A – 26th meeting of the CGPM,”.
[6] P J Mohr, D B Newell, B N Taylor, and E Tiesinga. 2018. “Data and analysis for the CODATA 2017 special fundamental constants adjustment,” Metrologia, vol. 55:125-146.
[7] Bureau International des Poids et Mesures – On the future revision of the SI. (2018, Sep.). [Online]. http://www.bipm.org/en/measurement-units/rev-si/
[8] BIPM. Bureau International des Poids et Mesures – Information for users about the proposed revision of the SI. [Online]. (2017, Jan.). Https://www.bipm.org/utils/common/pdf/SI-statement.pdf
[9] Joint CCM and CCU roadmap for the adoption of the revision of the International System of Units. [Online]. (2017, Jan.). https://www.bipm.org/utils/common/pdf/SIroadmap.
[10] M R Moldover, J P M Tusler, T J Edwards, J B Mehl, and R S Davis. 1988. “Measurement of the Universal Gas Constant R Using a Spherical Acoustic Resonator,” J. Res. Nat. Bur. Stand., vol. 93, no. 2, 85 – 144.
[11]. Segovia JJ, Lozano-Martín D, Martín MC, Chamorro CR, Villamañán MA, Pérez E, García Izquierdo C, del Campo D. 2017. Updated determination of the molar gas constant R by acoustic measurements in argon at UVa-CEM. Metrologia. 54:663–73.
[11]. Gavioso RM, Madonna Ripa D, Steur PPM, Gaiser C, Truong D, Guianvarc’h C, Tarizzo P, Stuart FM, Dematteis R. 2015. A determination of the molar gas constant R by acoustic thermometry in helium. Metrologia. 52:S274–304.
[12]. Pitre L, et al. 2017. New measurement of the Boltzmann constant k by acoustic thermometry of helium-4 gas. Metrologia. 54:856–73.
[13]. de Podesta M, Mark DF, Dymock RC, Underwood R, Bacquart T, Sutton G, Davidson S, Machin G. 2017. Re-estimation of argon isotope ratios leading to a revised estimate of the Boltzmann constant. Metrologia. 54:683–92.
[14]. Feng XJ, Zhang JT, Lin H, Gillis KA, Mehl JB, Moldover MR, Zhang K, Duan YN. 2017. Determination of the Boltzmann constant with cylindrical acoustic gas thermometry. Metrologia. 54:748–62.
[15]. Gaiser C, Fellmuth B, Haft N, Kuhn A, Thiele-Krivoi B, Zandt T, Fischer J, Jusko O, Sabuga W. 2017. Final determination of the Boltzmann constant by dielectric-constant gas thermometry. Metrologia. 54:280–9.
[16]. Qu JF, Benz SP, Pollarolo A, Rogalla H, Tew WL, White RD, Zhou KL. 2015. Improved electronic measurement of the Boltzmann constant by Johnson noise thermometry. Metrologia. 52:S242–56.
[17]. Flowers-Jacobs NE, Pollarolo A, Coakley KJ, Fox AE, Rogalla H, Tew WL, Benz SP. 2017. A Boltzmann constant determination based on Johnson noise thermometry. Metrologia. 54:730‑7.
[18]. Qu JF, Benz SP, Coakley KJ, Rogalla H, Tew WL, White RD, Zhou KL, Zhou ZY. 2017. An improved electronic determination of the Boltzmann constant by Johnson noise thermometry. Metrologia. 54:549–58.
[19]. Mejri S, Sow PLT, Kozlova O, Ayari C, Tokunaga SK, Chardonnet C, Briaudeau S, Darquié B, Rohart F, Daussy C. 2015. Measuring the Boltzmann constant by mid-infrared laser spectroscopy of ammonia. Metrologia. 52:S314–23.
[20]. Moretti L, Castrillo A, Fasci E, De Vizia MD, Casa G, Galzerano G, Merlone A, Laporta P, Gianfrani L. 2013; Determination of the Boltzmann constant by means of precision measurements of H218O line shapes at 1,39 μm. Phys Rev Lett. 111:060803.










[…] Link a la noticia completa […]