Martín López, Víctor – Canal de Isabel II, S. A.
Tejera López, Elena María – Canal de Isabel II, S. A.
ABSTRACT
The increasingly present effects of climate change, together with the expected population growth, are driving the emergence of strategies aimed at ensuring greater efficiency in the management of water demand.
Canal de Isabel II has developed a line of work, within the 2018-2030 Strategic Plan, aimed at guaranteeing the continuity of water supply. That means that the company makes actions to pursue that objective (Strategic Line 1).
To follow this objective, precision in the measurement of derived water is essential. That is, of the water that circulates through the channels from the reservoirs to the treatment stations.
To do this, we start from an initial situation in which there are 12 measuring stations within the Canal de Isabel II adduction network, from which the water level is measured continuously and precisely using ultrasonic limnimeters, connected with the Control Center of the company. From the level, the flow that circulates through the canal is obtained through flow curves, which result from the characterization of the measuring station.
The ISO Standards on free sheet flow measurement, necessary for the characterization of the measuring station, focus on open channels with unknown sections, giving the result with an accuracy of the order of 10 %.
This article describes the system to change the real curve used by Canal de Isabel II to obtain the flow from the height of the water in the open channel.
SUMARIO
Los efectos cada vez más presentes del cambio climático, unidos al esperado crecimiento de la población, están impulsando la aparición de estrategias destinadas a asegurar una mayor eficacia en la gestión de la demanda del agua.
En este sentido, desde Canal de Isabel II se ha desarrollado una línea de trabajo, dentro del Plan Estratégico 2018-2030, orientada a garantizar la continuidad del suministro a través de acciones que persiguen, entre otras cosas, la disminución del agua no controlada (Línea Estratégica 1).
Para el seguimiento de este objetivo es fundamental la precisión en la medida del agua derivada, es decir, del agua que circula por los canales desde los embalses a las estaciones de tratamiento.
Para ello, se parte de una situación inicial en la que se dispone de 12 estaciones de aforo dentro de la red de aducción de Canal de Isabel II, desde las que se mide, de manera continua y precisa, el nivel de agua mediante limnímetros ultrasónicos, conectados con el Centro de Control de la empresa. A partir del nivel se obtiene el caudal que circula por el canal a través de curvas de gasto, que resultan de la caracterización de la estación de aforo.
Las Normas ISO sobre medida del caudal en lámina libre, necesarias para la caracterización de la estación de aforo, se centran en canales abiertos con secciones desconocidas, dando el resultado con una precisión del orden del 10 %.
En esta segunda parte del artículo, continuación de la primera publicada en el número anterior, se va a tratar de explicar cómo a partir de las medidas experimentales realizadas con el método desarrollado se puede:
- Obtener el coeficiente de Manning para la introducción en la ecuación teórica.
- Obtener una curva de sexto grado para sustituir la que actualmente se usa para la obtención del caudal a partir de la altura de la lámina del canal.
PALABRAS CLAVE
Coeficiente de Manning, curva de sexto grado, estación de aforo, curva de gasto, altura de lámina, área mojada, velocidad media.
KEY WORDS
Manning coefficient, measuring station, flow rate, average velocity.
Introdución
Antecedentes
En la primera parte del artículo, que se presentó en el número anterior de esta misma revista, se describieron los antecedentes al artículo completo. Cabe destacar, entre los que se comentaron en ese momento y a modo de resumen, lo siguiente: Canal de Isabel II retoma en el año 2016 el proyecto “Aforos” con la intención de revisar las curvas de gasto de sus principales estaciones de aforo. Para ello, se realiza un estudio inicial con 8 aforos en la estación objeto del presente artículo (La Dehesa), empleando dos tipos de tecnologías distintas en busca del mejor método: un molinete universal y un perfilador Doppler por pulsos. En los resultados obtenidos se observa una gran dispersión entre las mediciones realizadas y el caudal calculado mediante la curva de gasto actual. Por ello, se establece la necesidad de revisar esta curva de gasto y la de aquellas Estaciones de aforo claves para Canal de Isabel II, empezando por las consideradas como prioritarias. La primera de ellas es la estación de aforo de La Dehesa, situada en el Canal del Atazar, y ubicada entre los municipios de Patones y Torrelaguna. Las medidas de caudal de este punto son prioritarias y altamente estratégicas para la compañía; de ahí la importancia de actualizar su curva de gasto. Este artículo describe el sistema que hemos empleado en Canal de Isabel II para la adecuación de la curva de gasto de un canal con una edad cercana a los 50 años.
Desarrollo
La realización de los aforos descritos en la primera parte de este artículo ha arrojado resultados discordantes entre los valores teóricos que están establecidos en el sistema SCADA que el Centro Principal de Control de Canal de Isabel II tiene para el cálculo del caudal en dicho punto del canal y los resultados de esos aforos. En el momento del inicio del estudio de la mejora de la medida en ese punto del canal, el sistema que se está utilizando es el de la obtención de un caudal a partir de una altura de lámina, medida ésta realizada con la precisión más elevada posible para medidas de esas características.
Estas alturas de lámina entran en el sistema a través de las comunicaciones pertinentes y es el propio SCADA el que se encarga de calcular el caudal resultante a partir de la curva establecida. Esta es una curva caracterizada por un polinomio de sexto orden con entrada altura de lámina y salida caudal. Cabe destacar en este punto que, aun tratándose de un canal muy extenso (alrededor de 50 km), Canal de Isabel II dispone de más puntos de medida que validan el estudio realizado y en ningún momento se compromete la gestión del abastecimiento y el uso racional del recurso. Esta caracterización, desarrollo del método explicado en el artículo anterior, y la corrección futura que se va a establecer amplían el conocimiento y corrigen una desviación conocida. Además de estos beneficios, el conocimiento en la medida de velocidad/caudal en lámina libre es siempre un reto apasionante para los profesionales que nos dedicamos a la medida de estas magnitudes. La ampliación del conocimiento de la medida del caudal en lámina libre será redundante con otras acciones para la mejora de la gestión del recurso hídrico, tan escaso en la región de Madrid.
A continuación, se muestra a modo informativo la tabla comparativa obtenida. Esta tabla, está construida de la siguiente manera:
- En primer lugar (columnas 1 a 4) los valores auxiliares de las medidas realizadas: fecha, altura de lámina, velocidad media calculada y repetibilidad.
- A continuación, se representa el caudal obtenido con el molinete. Valor obtenido en base al sistema de cálculo descrito en la primera parte del artículo.
- Después se representa el valor que el sistema SCADA ofrece en función de los parámetros altura de lámina y curva de gasto programada.
- Y, por último, se representa el valor relativo de desviación entre ambas “medidas”.
MÉTODO MEDIDA EN AFORO: MOLINETE SECCIÓN CENTRAL
| Fecha | Nivel (m) | v media (m/s) | Repetibilidad | Q (m3/s) Sección topógrafos | Q (m3/s) Curva de gasto | Molinete vs. Curva de gasto |
| 18/01/2018 | 1,08 | 1,21 | -0,349 % | 3,933 5 | 4,174 3 | -5,77 % |
| 22/02/2018 | 1,54 | 1,53 | 1,081 % | 7,697 9 | 7,675 8 | 0,29 % |
| 15/03/2018 | 1,50 | 1,51 | -0,098 % | 7,122 9 | 7,360 6 | -3,23 % |
| 10/05/2018 | 1,63 | 1,57 | -0,108 % | 8,062 1 | 8,382 2 | -3,82 % |
| 07/06/2018 | 1,46 | 1,49 | 0,951 % | 6,779 4 | 7,045 5 | -3,78 % |
| 21/06/2018 | 1,82 | 1,63 | 0,252 % | 9,410 1 | 9,835 3 | -4,32 % |
| 18/10/2018 | 1,61 | 1,55 | -0,233 % | 7,855 9 | 8,225 8 | -4,50 % |
| 07/11/2018 | 1,55 | 1,52 | -0,811 % | 7,364 5 | 7,754 6 | -5,03 % |
| 31/01/2019 | 1,50 | 1,49 | 0,610 % | 6,988 3 | 7,360 6 | -5,06 % |
| 27/06/2019 | 1,90 | 1,65 | -1,330 % | 9,957 2 | 10,420 9 | -4,45 % |
| 11/09/2019 | 1,76 | 1,61 | 0,660 % | 8,926 7 | 9,384 5 | -4,88 % |
| 17/10/2019 | 1,46 | 1,45 | -0,276 % | 6,635 3 | 7,045 5 | -5,82 % |
| 30/10/2019 | 1,55 | 1,5 | 0,623 % | 7,276 9 | 7,754 6 | -6,16 % |
Como se puede comprobar la desviación entre las dos medidas está en el entorno del 4,7 % de media.
A la vista de las cifras obtenidas, se decide corregir la desviación en la medida programada actualizando la curva de gasto.
Para la actualización de la curva de gasto de la estación de aforo de La Dehesa se han valorado 3 opciones:
- Curvas analíticas: Se ajusta la curva de gasto con expresión analítica concreta.
- Basadas en fundamentos hidráulicos con parámetros físicos o
- Fórmula matemática con parámetros abstractos a ajustar.
- Empleo de modelos numéricos de flujo en lámina libre: Para este sistema hay que obtener pares nivel-caudal a partir de cálculos con modelos, con lo que la curva se define como una poli-línea.
- Fórmula de Manning: Este sistema tiene en cuenta fundamentalmente lo siguiente:
- Pendiente de energía / pendiente geométrica
- Rugosidad.
El primer sistema está enfocado para otras características de medidas en lámina libre y aunque podríamos optar por el segundo si se modelizaran los canales, se ha decidido obtener la curva de gasto utilizando la fórmula de Manning.
Obtención de la curva de gasto
Método de la Curva de Manning
La fórmula de Manning es la siguiente:
\(v=\frac{1}{n}*Rh^{\frac{2}{3}}*I_{0′}^{\frac{1}{2}};I_{0}=\frac{n^{2}*v^{2}}{Rh^{\frac{3}{4}}}\)
(1)
\(Rh=\frac{A}{pm}=\frac{\mathrm{\acute{A}rea}}{\mathrm{Per\acute{\imath}metro~mojado}}\)
(2)
\(Q=v*A\)
(3)
\(Q=\frac{1}{n} * A * Rh^{\frac{2}{3}}*I_{0}^{\frac{1}{2}}\)
(4)
Donde I0 es la pendiente geométrica (solera del canal)
n = coeficiente de Manning
v = velocidad
Rh = Radio hidráulico
Dicho parámetro (I0) se obtuvo en el levantamiento topográfico realizado en la Estación de aforo.
Por tanto, y a la vista de las ecuaciones antes expresadas, el único parámetro que hay que obtener es el coeficiente de Manning. Aun teniendo en cuenta que existen valores experimentales teóricos que podríamos aplicar, es cierto que la obtención de este parámetro es posible debido a todas las medidas realizadas con el molinete. Además, teniendo en cuenta la antigüedad del canal, hemos considerado pertinente calcularlo.
De manera que, para la obtención de dicho parámetro, se ha empleado el método de minimizar el error obtenido con el cálculo del caudal usando la fórmula de Manning y el caudal obtenido en la realización de aforos experimentalmente.
\(\mathbf{Q(n)-Q(aforo)\rightarrow 0}\)
(5)
Utilizando la función minimizar error en el programa Microsoft Excel, se han obtenido los siguientes valores, calculados con un valor de coeficiente resultante de:
n = 0,012 5
| Q (aforo) (m3/s) | Q (n) (m3/s) |
| 3,933 5 | 4,332 1 |
| 7,697 9 | 7,357 9 |
| 7,122 9 | 7,089 1 |
| 8,062 1 | 7,958 4 |
| 6,779 4 | 6,820 5 |
| 9,410 1 | 9,244 1 |
| 7,855 9 | 7,829 8 |
| 7,364 5 | 7,425 4 |
| 6,988 3 | 7,089 1 |
| 9,957 2 | 9,777 4 |
| 8,926 7 | 8,841 3 |
| 6,635 3 | 6,820 5 |
| 7,276 9 | 7,425 4 |
En la referencia bibliográfica el libro: Hidráulica de los canales abiertos. Ven Te Chow. 1982
https://wwwrcamnl.wr.usgs.gov/sws/fieldmethods/Indirects/nvalues/ se establece la siguiente tabla de valores teóricos de coeficiente de Manning.
| N de Manning | Denominación |
| 0,027 | canal en tierra, recto y uniforme, excavado o dragado, con pastos cortos y algunas malezas |
| 0,033 | canal revestido, fondo de gravas con lados de piedra suelta o riprap |
| 0,025 | canal revestido, mampostería, piedra suelta cementada |
| 0,013 | canal revestido, hormigón terminado con llana metálica (palustre) |
El canal de estudio es exactamente un canal revestido, con hormigón terminado con llana metálica (palustre). Por lo que, la obtención por métodos experimentales de un valor tan cercano al publicado en bibliografía, y suponiendo que el valor publicado es certero, ahonda en el hecho de que las medidas experimentales realizadas tienen una precisión que no deberá distar en valor relativo de lo que se ha obtenido de diferencia en el coeficiente de Manning. Esta es otra conclusión y validación del método descrito en el primer artículo.
La representación gráfica de la curva propuesta vs. la curva actual quedaría de la siguiente forma:
Y en expresión matemática:
\(Q=\frac{1}{n} * A * Rh^{\frac{2}{3}}*I_{0}^{\frac{1}{2}}\)
(6)
Donde: n = 0,0125
I0 = 0,00040497
\(Q= 1,60726704* A *Rh^{\frac{2}{3}}\)
(7)
La ecuación 7, representada en la figura 2, tiene las siguientes particularidades:
- Únicamente sirve para el tramo medido experimentalmente H(m) ϵ (1,08; 1,90)
- Para utilizarla hay que introducir en SCADA la matriz de (H, Rh) para interpolar con cada H.
- Posiblemente esta curva no sea válida cuando la sección está próxima al llenado: efecto del aire, posibles problemas de entrada en carga. Dicho efecto habría que comprobarse con más medidas en campo efectuadas en los puntos críticos.
Obtención de la curva basada en un polinomio de sexto grado a partir de la Curva de Manning
El SCADA del Centro de Control de Canal de Isabel II está parametrizado en estos momentos, como ya se ha dicho, con una curva cuyo origen es un polinomio de sexto grado. El siguiente paso, por tanto, para la corrección del valor de la curva de gasto es precisamente obtener estos coeficientes.
De forma análoga a como se realizó el cálculo del coeficiente de Manning, se han obtenido estos resultados:
| La Dehesa nuevo | |
| Coef 0 | 0,000 000 000 0 |
| Coef 1 | 1,611 047 621 4 |
| Coef 2 | 0,127 215 857 6 |
| Coef 3 | 4,426 180 250 2 |
| Coef 4 | -3,198 765 989 1 |
| Coef 5 | 0,881 702 738 9 |
| Coef 6 | -0,088 969 194 0 |
Representando gráficamente las dos curvas, se puede comprobar la escasa diferencia entre ambas, así como con los puntos aforados experimentalmente.
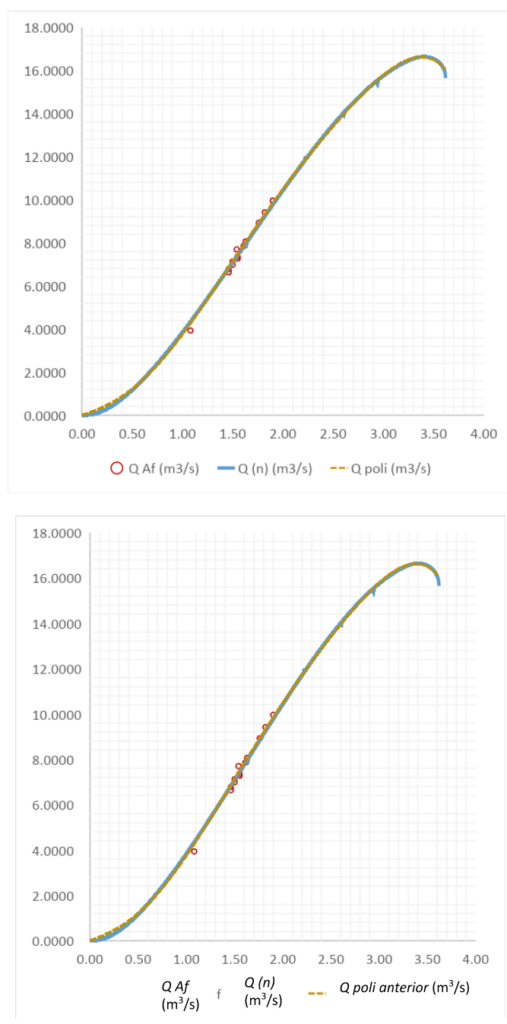
Conclusión
Las principales conclusiones obtenidas en este trabajo son las siguientes:
- La obtención, a partir de un sistema experimental, del coeficiente de Manning no hace más que validar el sistema de obtención de dichas medidas.
- La ejecución de medidas experimentales por el sistema descrito a lo largo del tiempo está justificada para validar las medidas y controlar las efectuadas por otros sistemas. Estas medidas pueden ir variando en el tiempo, y son directamente dependientes del estado del canal.
- El canal en el que se ha realizado el estudio, y su estación de aforo de La Dehesa más concretamente, se encuentra en un estado de conservación muy bueno, dada la proximidad entre el coeficiente de Manning experimental y el teórico.
Referencias
– UNE-EN ISO 748, (2009) Medida de caudal de líquidos en canales abiertos utilizando medidores de caudal o flotadores. Versión oficial en español, de la Norma Europea EN ISO 748:2007, que a su vez adopta la Norma Internacional ISO 748:2007.
– UNE-EN ISO 18365, (2014) Selección, establecimiento y operación de una estación de aforo. Versión oficial en español, de la Norma Europea EN ISO 18365:2013, que a su vez adopta la Norma Internacional ISO 18365:2013.
– VEN TE CHOW, Ph. D, (1999) Hidráulica de canales abiertos. Edición de Martha Edna Suárez R. Santafé de Bogotá, McGraw-Hill.
– OMM 2010-1.- Manual on Stream Gauging. Volume I – Fieldwork. WMO-No. 1044. 2010.- OMM 2010-2.- Manual on Stream Gauging. Volume II – Computation of Discharge. WMO-No. 1044. 2010.










Comentarios