Gabriel Peñas Civit
Ingeniero-Inspector de la Sección de Metrología
Servicio de Automóviles, Metrología y Productos
Dirección General de Industria
Departamento de Empresa y Trabajo
Generalitat de Catalunya
Resumen:
Existe una gran variedad de productos envasados en el mercado que son fabricados en serie y destinados a su venta en cantidades nominales unitarias constantes. Los envasadores de estos productos deben asegurar una cantidad mínima de producto dentro de los envases y una manera de hacerlo es tomar muestras de los lotes y estimar, a partir de los datos obtenidos, la cantidad que se está envasando y la proporción de elementos con déficit de llenado encontrados. Para que la estimación sea válida para representar el comportamiento de la producción, la normativa define ciertos parámetros de control estadístico. En este artículo se describe como comparar la eficacia de distintos métodos de control estadístico con el descrito en el Real Decreto 1801/2008, de 3 de noviembre, por el que se establecen normas relativas a las cantidades nominales para productos envasados y al control de su contenido efectivo.
Palabras clave:
Envasado, contenido efectivo, eficacia, plan de muestreo, control estadístico, lote y tamaño de muestra.
Abstract:
There is a wide variety of packaged products on the market that are mass-produced and sold in constant nominal unit quantities. The packers of these products must ensure a minimum amount of product inside the packaging and one way to do this is to take samples of the batches and estimate, based on the data obtained, the quantity that is being packaged and the proportion of items with shortfall. For the estimate to be valid to represent the behaviour of production, the regulations define certain parameters of statistical control. This article describes how to compare the efficacy of different statistical control methods with that described in the regulations “Royal Decree 1801/2008”, of November 3, which establishes rules regarding nominal quantities for packaged products and their control.
Keywords:
Packaging, effective content, efficiency, sampling plan, statistical control, batch and sample size.

Introducción:
Existe una gran variedad de estudios sobre planes de muestreo y métodos de control estadístico, de los cuales, solamente nos centraremos en el que utiliza la normativa en relación a las cantidades envasadas. La Directiva del Consejo de 20 de enero de 1976 (76/211/CEE) [1], fue modificada en los años 1978, 2007 y 2019. En esta última modificación se cambia el artículo 6, donde se faculta a la Comisión la modificación de los anexos I y II para adaptarlos al progreso técnico y se añade el artículo 6 bis, donde se definen los periodos de control, los informes, la delegación de poderes y las responsabilidades respecto al Parlamento Europeo y al Consejo. En estos dos anexos se definen los planes de muestreo de referencia que se adoptaron al ordenamiento jurídico español mediante el Real Decreto 1801/2008, de 3 de noviembre [2]. En adelante, para facilitar la lectura y comprensión del texto, nos referiremos a esta normativa como real decreto. Este real decreto da cumplimiento a la Directiva 2007/45/CE [3], y en consecuencia a la Directiva 76/211/CEE.
Antes de empezar con la estadística, comentar que las medidas de las muestras en los ensayos, deben ser fiables. Para ello, los datos utilizados para realizar el control estadístico de lotes, deben ser medidas realizadas con instrumentos idóneos a las cantidades o formatos que se envasan (art. 13 del real decreto) y sometidos al control metrológico del Estado (art. 14 del real decreto). Para comprobar la idoneidad de estos instrumentos podemos consultar el artículo: “La idoneidad de los instrumentos de control utilizados por los envasadores en el etiquetado del contenido de productos envasados.” [4], publicado en la revista e-medida nº13, en marzo de 2018. Estos instrumentos, utilizados para medir o controlar el contenido efectivo de los productos envasados, a partir de los dos años de su puesta en servicio, deben realizar verificaciones periódicas para comprobar y confirmar que mantienen sus requisitos reglamentarios. También se realizará una verificación después de una reparación o una modificación del instrumento. El control metrológico de los instrumentos de pesaje de funcionamiento automático, o de funcionamiento no automático, cuando están en servicio, se regulan por la Orden ICT/155/2020, de 7 de febrero [5]. Que los instrumentos mantengan sus errores máximos permitidos cuando están en servicio y que sean idóneos a las cantidades a envasar, será indispensable para poder estimar la cantidad efectiva que se envasa.
En primer lugar, debemos recordar que el envasador puede escoger entre medir o controlar el contenido efectivo, tal como indica el artículo 14.2 del mismo real decreto. Si por el tipo de producto, formato, personal técnico, instrumentos de medida u otros criterios, el envasador decide medir el contenido efectivo en lugar de controlarlo, entonces el contenido efectivo de cada uno de los envases deberá ser igual o superior a la cantidad nominal indicada en el envase. Cuando se mide no es necesario realizar el control estadístico a no ser que estos productos lleven el marcaje CE “e”.
En segundo lugar, comentar el artículo 9. c) del real decreto. El marcado del envase con el signo CE “e”, nos indica que el envase ha seguido las modalidades de control estadístico de lotes establecidas en el real decreto, o de eficacia comparable1, y cumple con las disposiciones del mismo. Esto condiciona el tamaño de lote, que como indica en el artículo 3.h), cuando el control de los envases se realiza al final de la cadena de envasado, el tamaño del lote es igual a la producción horaria máxima. Por lo tanto, habrá que realizar el muestreo que indica el artículo 11 y el del artículo 12 por cada hora de producción. Este hecho hace que la empresa deba dedicar varias horas de un trabajador para realizar el control del contenido efectivo o disponer de un instrumento de pesaje automático que registre los datos de los controles cada hora de producción y rechace automáticamente los productos con cierto déficit de llenado.
En tercer lugar, comentar que las empresas que optan por controlar el contenido efectivo, pueden ajustar mejor la media del contenido efectivo a la cantidad nominal y tener menos pérdida de material. Considerando también que, aunque el resultado del control de la media del contenido efectivo del artículo 12 del real decreto pueda ser aceptado con un valor ligeramente inferior a la media por unos lotes discretos, el envasado se realizará de tal forma que la media del contenido efectivo de los envases no sea inferior a la cantidad nominal, cumpliendo así con el artículo 7.a) de la misma normativa. Por consiguiente, habrá lotes con medias de contenido efectivo superior al valor de la cantidad nominal que compensen los que tienen déficit. Los servicios de inspección podrán solicitar los registros de los controles para comprobar que no se esté envasando por debajo de la cantidad nominal.
En cuarto lugar, tal como se menciona en el artículo “Diseño de una campaña de inspección de fábricas y plantas de envasado de productos envasados con cantidades nominales expresadas en unidades de masa” [6], publicado en la revista e-medida nº 6, en junio de 2014, en referencia a la parte de la elección del procedimiento, recordar que el envasador no está obligado a utilizar un procedimiento de control que siga las modalidades previstas en el artículo 10 del real decreto, si no lo hace, debe usar otro con una eficacia comparable igual o superior y ser capaz de demostrar que cumple dicha condición”. A partir de ahora supondremos que el envasador quiere controlar el contenido efectivo de sus envases, quiere realizar un control estadístico distinto al descrito en el real decreto y que sea de eficacia comparable.


Desarrollo
1. Curva de eficacia de un plan de muestreo
En la elaboración de un plan de muestreo se puede definir el tamaño de lote, el nivel de inspección (especial SI, SII, SIII, SIIII o general I, II, III), el plan de muestreo (si se toma una muestra o más por lote), el tipo de inspección (normal, estricta o reducida), el tamaño de la muestra (n) y los criterios de aceptación y rechazo. Según el procedimiento de la Norma UNE-ISO 2859, no siempre se realizará el mismo muestreo, cambiará el tamaño de muestra o el criterio según el resultado del control de las muestras anteriores. Volvemos a recordar que el envasador puede definir su propio plan de muestreo y procedimiento de control estadístico, mientras sea de eficacia comparable al que realiza el real decreto
Un plan de muestreo por lotes consiste en tomar una o varias muestras de cada lote, inspeccionar esas muestras y estimar la calidad de la producción. La curva de eficacia, o llamada también curva característica de operación, para un plan de muestreo por atributos, nos permite representar en un gráfico la probabilidad de aceptación de nuestro lote, en relación al porcentaje de unidades defectuosas (con déficit de llenado) encontradas en la muestra representativa. Para un plan de muestro por variables nos representa la probabilidad de aceptación del lote en proporción al mal funcionamiento de la media. Esta curva de operación nos servirá para poder comparar la eficacia de distintos planes de muestreo. A continuación, un ejemplo de curva de eficacia de un plan de muestreo por atributos.
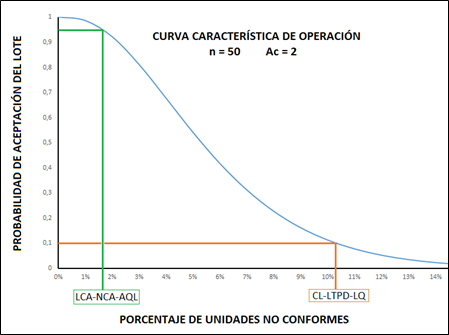
Observamos que cuando el gráfico se acerca más al eje de ordenadas, menor es la proporción de unidades defectuosas y mayor la probabilidad de aceptación del lote. Realizaremos un gráfico para el plan de muestreo por atributos y un gráfico para el plan de muestreo por variables, que serán comparables al control estadístico del real decreto según lo previsto en el artículo 15, puntos 2 y 3, respectivamente.
El grafico representado en la figura 1 es la curva característica de operación para un control por atributos, donde el tamaño de muestra son 50 envases y el criterio de aceptación es 2. El número de aceptación, o criterio de aceptación, es el número máximo de unidades de producto no conformes, con déficit de llenado, que podemos encontrar en la muestra y dar por válido el lote. El número de rechazo es el número mínimo de unidades no conformes que dan por nulo el lote. El porcentaje de unidades de producto con déficit de llenado se define como porcentaje de no conformidad. LCA (Nivel de Calidad Aceptable), en una serie continua de lotes, es el límite medio del proceso satisfactorio, dicho de otra forma, la calidad media deseada. El término NCA, nivel de calidad aceptable, a partir de la Norma UNE ISO 2859-2:2012, es sustituido por LCA. En tablas lo encontraremos también con las siglas en inglés AQL (Acceptable Quality Limit). La calidad media no deseada será el valor CL (Calidad Límite) o LTPD (Lot Tolerance Percent Defective), se define para lotes aislados y tiene una baja probabilidad de aceptación del lote.
2. Eficacia del plan de muestreo definido en el Real Decreto
El real decreto da cumplimiento a la Directiva 2007/45/CE del Parlamento Europeo y del Consejo, en la cual se derogan las Directivas 75/106/CEE y 80/232/CEE del Consejo y se modifica la Directiva 76/211/CEE del Consejo. El anexo II de la Directiva 76/211/CEE, antes de la modificación del año 1978, hacía referencia a la Norma ISO 2859, relativa a los métodos de prueba por atributos, en la que se utilizaba un nivel de calidad aceptable del 2,5 %. El nivel de muestreo correspondía, en caso de pruebas no destructivas, al nivel II de dicha norma, y en el caso de pruebas destructivas al nivel S. 3. Actualmente la eficacia del método de referencia es la utilizada por el método del anexo II de la Directiva 76/211/CEE o la definida por los planes de muestreo del artículo 11 y 12 del real decreto. Las guías WELMEC [7] y las guías OIML [8] desarrollan el control del envasado y nos pueden ayudar a comprender mejor los cálculos y procedimientos.
Se realizará un plan de muestreo por atributos, basado en características de tipo cualitativas (pasa/no pasa) y también un plan de muestreo por variables, basado en características cuantitativas (peso o volumen). El real decreto realiza un plan de muestreo por atributos en el artículo 11 y un plan de muestreo por variables en el artículo 12.
3. Plan de muestreo por atributos
Para un muestreo simple por atributos utilizaremos la siguiente función2 para hallar la probabilidad de aceptación del lote “PA”:
\(P_{A(p)}=\sum_{i=0}^{i=c}{C_{n}^i}\cdot p^i\left(1-p\right)^{n-i}\)
- PA: probabilidad de aceptación
- n: tamaño de la muestra
- c: número máximo admisible de unidades defectuosas que acepta el lote
- p: porcentaje de unidades defectuosas del lote
\(P_A=\sum_{i=0}^{i=c_1}{C_{n1\ }^i}\cdot p^i\left(1-p\right)^{n_1-i}+\\ \left[\sum_{i=c_1+1}^{{i=r}_1-1} \left(C_{n1}^ip^i\left(1-p\right)^{n1-i}\ast\sum_{j=0}^{j=c2-i}{C_{n1+n2\ }^jp^j\left(1-p\right)^{\left(n1+n2\right)-j}}\right)\right]\)
Y para un plan de muestreo doble, por atributos, tendremos la siguiente función3 de probabilidad de aceptación del lote:
- c1: número máximo admisible de unidades defectuosas en la primera muestra
- r1: número de unidades defectuosas en la primera muestra que rechaza el lote
- c2: número máximo admisible de unidades defectuosas acumuladas en ambas muestras
- c1 ≤ r1 ≤ c2
Ejemplo A.
En el siguiente ejemplo, el tamaño del lote del envasador son 150 envases y la muestra aleatoria representativa son n = 15 envases. El criterio de aceptación para el envasador es c = 0. Esto significa que no podemos encontrar ni un solo envase con defecto de llenado para aceptar el lote. Un producto tiene déficit de llenado cuando el contenido efectivo es inferior al contenido mínimo tolerado. El real decreto realiza un plan de muestreo simple para el ensayo destructivo y un doble plan de muestreo para el ensayo no destructivo. Supondremos en los ejemplos A y B que por el tipo de producto debemos realizar ensayos destructivos. Hallaremos las curvas características de operación empleando una hoja de cálculo de un ordenador y después podremos comparar la eficacia de los planes de muestreo. Realizaremos dos cuadros de datos y después realizaremos el gráfico.
1. En el cuadro A1 introduciremos las condiciones. Los tamaños de muestra y los criterios de aceptación que nos indica el real decreto y el envasador.
CUADRO A1
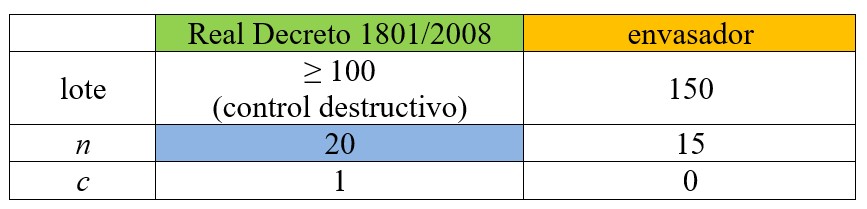
2. En el cuadro A2 indicaremos la proporción de elementos defectuosos X y calcularemos la probabilidad de aceptación del lote para cada tamaño de muestra utilizando la fórmula:
\(P_{A(p)}=\sum_{i=0}^{i=c}{C_{n\ }^i}\cdot p^i\left(1-p\right)^{n-i}\)
CUADRO A2
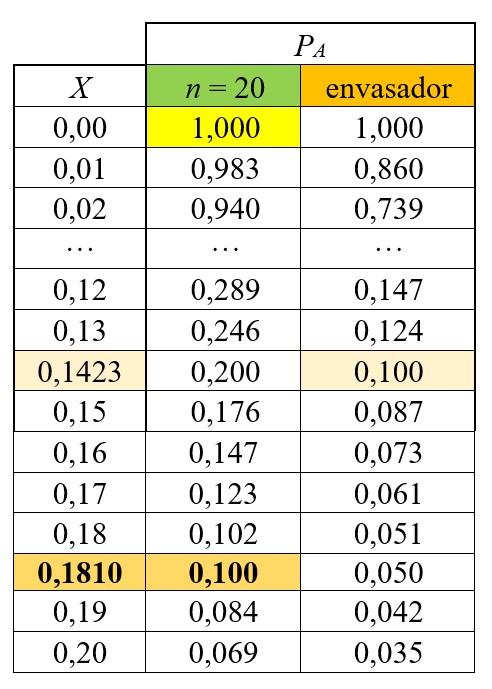
En la casilla pintada en amarillo del cuadro A2 escribiremos la fórmula de la distribución binomial, la cual copiaremos arrastrando la esquina de la misma casilla hacia al resto de casillas de la misma columna. Por ejemplo, tendremos como resultado de aplicar la fórmula de la distribución binomial, en las dos primeras casillas (para muestra de 20 envases) el siguiente resultado:

donde la casilla:
- C5, será la casilla del cuadro A1, correspondiente al criterio de aceptación que marca el real decreto para la muestra de 20 unidades, es decir, el número máximo admisible de unidades defectuosas que acepta el lote para esa muestra, correspondiente a “1”.
- C4 será el tamaño de la muestra, correspondiente a “20”.
- B12 y B13 serán las casillas con los primeros valores de X, correspondientes a “0,00” y “0,01” que representan un porcentaje de envases defectuosos del 0 % y del 1 %.
- VERDADERO significa que la distribución es acumulada.
El símbolo $ sirve para mantener los mismos valores (casillas) al arrastrar la fórmula. Realizaremos la misma operación con las distintas columnas hasta obtener el cuadro A2 completo.
3. Realizamos el gráfico.
Para representar el gráfico simplemente seleccionaremos todos los valores de X y todos los valores calculados de probabilidad a la vez, iremos a la pestaña insertar y escogeremos el gráfico de dispersión.
Figura 2
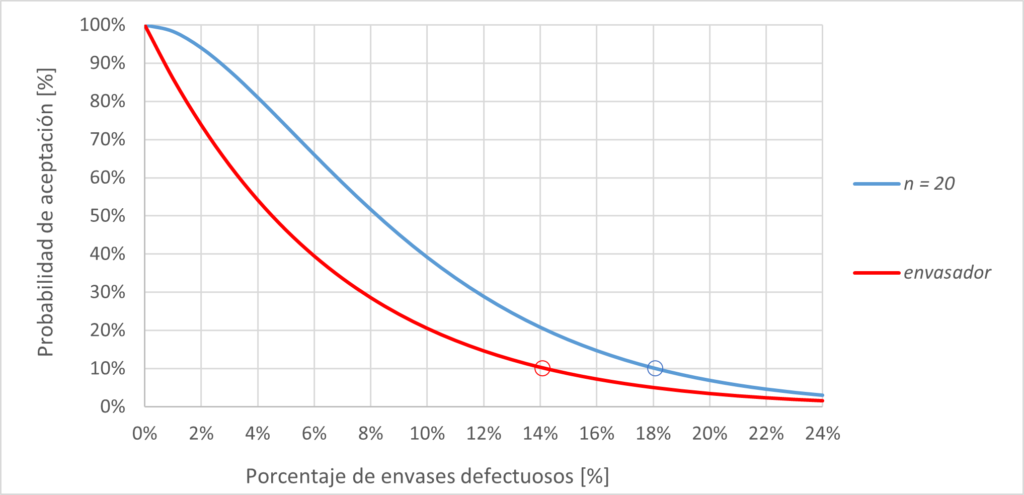
Observamos que, al aumentar el tamaño de muestra, la curva característica de operación se desplaza hacia el eje de ordenadas y, por lo tanto, para una misma probabilidad de aceptación del lote, hallaremos menos envases con déficit de llenado.
4. Definimos los porcentajes X10r y X10i:
- X10r es el porcentaje de unidades defectuosas aceptadas con una probabilidad del 10 % en el control de referencia, calculado a partir de la ecuación de la curva característica de operación o determinado con los valores del gráfico. Figura 2.
- X10i es el porcentaje de unidades defectuosas aceptadas con una probabilidad del 10 %, en un control distinto al de referencia, calculado a partir de la ecuación de la curva característica de operación o determinado con los valores del gráfico, figura 2.
Un plan de muestreo por atributos será comparable al definido en el real decreto cuando:
– la diferencia entre el porcentaje de unidades defectuosas X10i aceptadas por un plan de control distinto al de referencia y el porcentaje de envases defectuosos X10r aceptado por el control de referencia, no supere el 15 % del porcentaje de envases defectuosos X10r del método de referencia.
Esta condición se puede expresar de la siguiente forma4:
| X10i – X10r | < 15 % X10r .
Comparamos la curva de eficacia de color rojo con la azul. Cuando la probabilidad del método de referencia es del 10 %, el porcentaje de envases defectuosos es X10r =18,10 %. Para la curva del envasador, el porcentaje de envases defectuosos, cuando la probabilidad de aceptación del 10 %, es X10i = 14,23 %.

5. Aplicamos la fórmula: | X10i – X10r | < 15 % X10r
|14,23-18,10| < (0,15 · 18,10) ➔ 3,869> 2,715 ➔ No cumple.
El plan de muestreo del ejemplo A no es de eficacia comparable al del real decreto.
Ejemplo B.
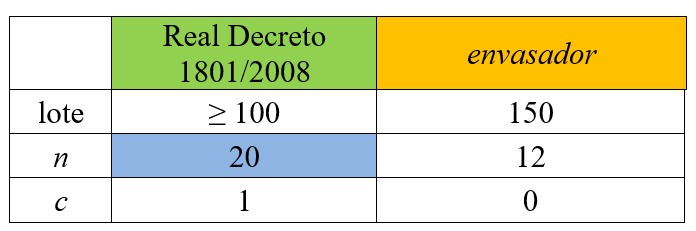
En este ejemplo utilizamos el mismo tamaño de lote de 150 envases, el mismo criterio de aceptación “0” y cambiamos el tamaño de muestra a 12 envases.
1. En el cuadro A1 modificaremos el tamaño de muestra a 12 envases y automáticamente nos cambiará el cuadro de datos y el gráfico. Supondremos también ensayo destructivo.
CUADRO B1
2. El programa calcula las nuevas probabilidades de aceptación y obtenemos los siguientes resultados:
CUADRO B2
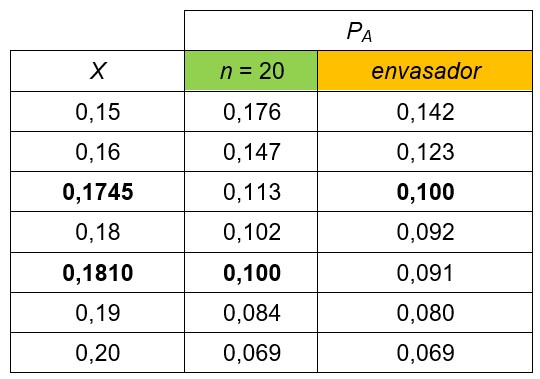
3. Aplicando la fórmula anterior:
| X10i – X10r | < 15 % X10r ➔ |17,45 – 18,10| < (0,15 · 18,10) ➔ 0,65 < 2,715 ➔ Cumple
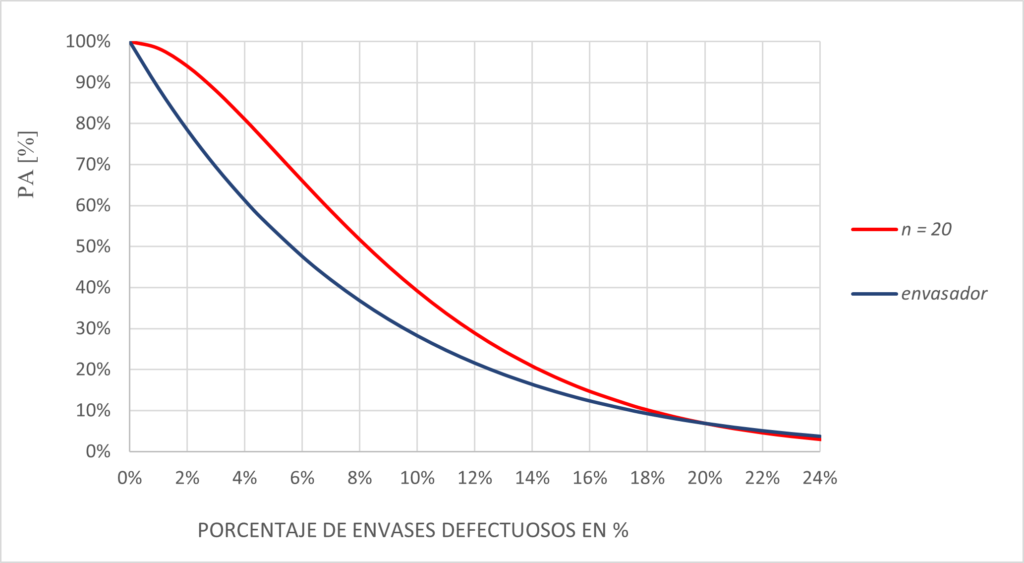
El plan de muestreo por atributos del ejemplo B es de eficacia comparable al plan de muestreo por atributos que realiza el real decreto. En el siguiente gráfico se muestran las dos curvas.
Figura 3.
4. Plan de muestreo por variables
Para un muestreo simple por variables utilizaremos la siguiente función5 para hallar la probabilidad de aceptación del lote “PA”:
\(P_{A(\lambda )} = F\left[t_{1-\alpha}-\left(\lambda\cdot\sqrt n\right)\right]\)
donde:
- PA: probabilidad de aceptación
- F: función de distribución acumulativa de la variable “t” de Student de cola izquierda.
- t1-α: función inversa de la variable “t” de Student para un nivel de confianza (1-α) con (n-1) grados de libertad.
- (1-α): nivel de confianza de la prueba. (1 – α) = 0.995 según Directiva (76/211/CEE)
- λ: proporción de mal funcionamiento de la media
- n: tamaño de la muestra
Ejemplo C.
En el siguiente ejemplo, un envasador quiere saber si la eficacia de su plan de muestreo por variables es comparable al que realiza el real decreto. El envasador produce en lotes de 450 unidades. Por cada lote toma una muestra de 17 unidades. El riesgo del control es del 0,8 % (β = 0,008). El valor β es el error aleatorio (o nivel de significancia) y representa el número de intervalos sobre 100 que no contienen el valor deseado de la media. Para que sean comparables, el plan de muestreo del envasador tendrá un nivel de confianza igual o superior al de referencia.
Cuando el tamaño de la muestra es pequeño, la distribución de probabilidad de t de Student nos sirve para estimar la media de una población que sigue una distribución normal. En relación a la probabilidad de aceptación, comentar que la función mide lo alejada que está la media del valor medio. Como solamente nos interesa saber la probabilidad que la media esté en déficit, nos fijaremos solamente en la cola izquierda de la función. Así tendremos que α = β/2.
| Plan de muestreo envasador: | β = 0,008 | α = 0,004 | 1-α = 0,996 |
| Plan de muestreo real decreto: | β = 0,01 | α = 0,005 | 1-α = 0,995 |
Para representar el gráfico y poder comparar la eficacia de cada curva, será necesario realizar dos cuadros.
1. En el cuadro C1 indicamos las siguientes condiciones:
CUADRO C1
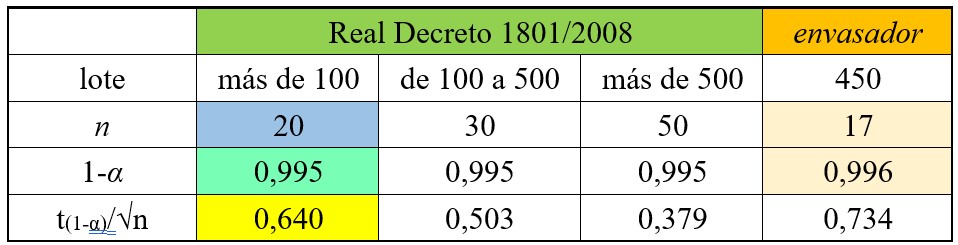
La última fila nos sirve para establecer el criterio de aceptación y rechazo, siempre que el método sea comparable. Se calcula la t de Student (con tamaño de muestra y grados de libertad ya definidos) y dividimos el resultado por la raíz del tamaño de muestra. Por ejemplo, para la casilla amarilla del cuadro C1, utilizamos la función que devuelve el inverso de la distribución t de Student de cola izquierda y añadimos el símbolo “$” para mantener los mismos valores cuando realicemos el cuadro C2 y calculemos todas las probabilidades.

Donde:
- la casilla C5 (verde) es el nivel de confianza de la prueba, y
- la casilla C4 (azul) es el tamaño de muestra.
2. Indicaremos la proporción de la característica bajo control λ, que representa el mal funcionamiento de la media y calcularemos la probabilidad de aceptación del lote para cada tamaño de muestra y nivel de confianza con la función:
\(PA(\lambda ) = \mathrm{F}\left[t_{1-\alpha}-\left(\lambda\cdot\sqrt n\right)\right]\)
CUADRO C2
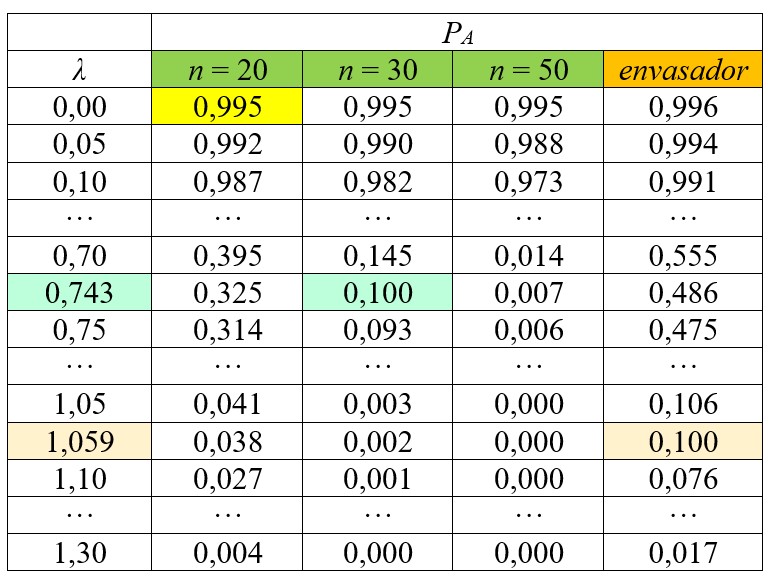
Realizamos el cálculo en la hoja de cálculo de la siguiente manera:
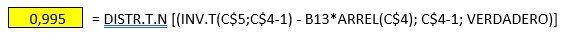
La función F, para el cálculo de la probabilidad de aceptación, PA = F[x], es la distribución normal de la “t de Student” de cola izquierda con las siguientes variables: (x, grados de libertad, acumulada), donde \(\left[x\right]= \left[t_{1-\alpha}-\left(\lambda\cdot\sqrt n\right)\right]\). Cuando mayor sea λ, más alejada estará la media del valor nominal y menor será la probabilidad de aceptación.
3. Gráfico.
Para representar el gráfico simplemente seleccionaremos todos los valores de y todos los valores calculados de probabilidad a la vez, iremos a la pestaña insertar y escogeremos el gráfico de dispersión.
Figura 4
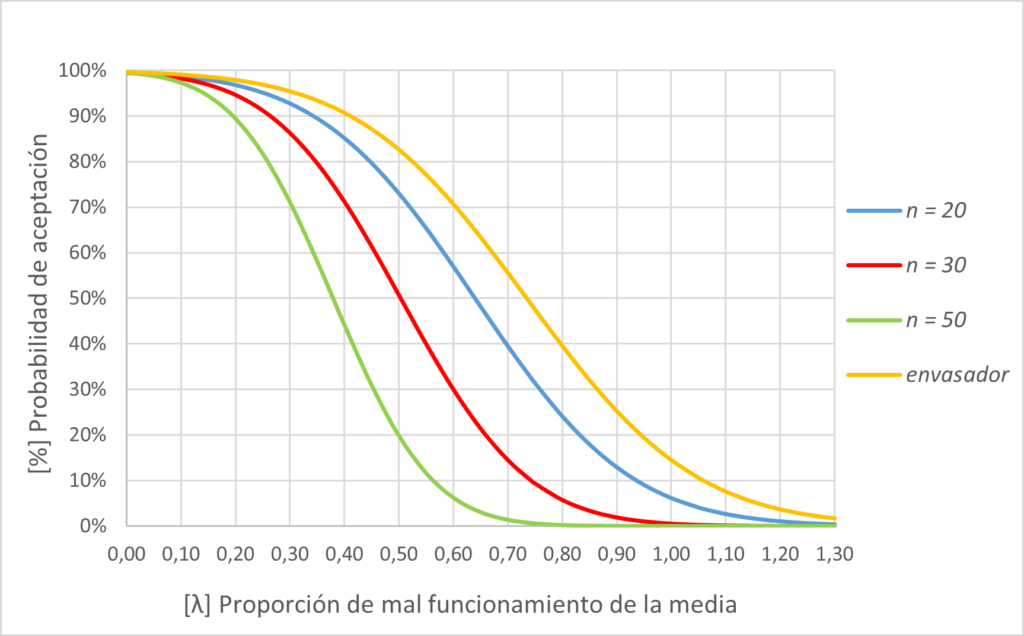
Observamos que, para un mismo nivel de confianza, a mayor tamaño de muestra, la curva característica de operación se acerca más al eje de ordenadas y, por consiguiente, la media tiene mayor probabilidad de aceptación.
4. Obtendremos los valores lambda [λ]:
- λ10i: valor del eje de abscisas aceptado para un control alternativo con 10 % de probabilidad de aceptación.
- λ10r: valor del eje de abscisas aceptado para el control de referencia con un 10 % de probabilidad de aceptación.
Un plan de muestreo por variables será comparable al definido en el real decreto cuando:
- Teniendo en cuenta las curvas características de operación, el valor λ del método alternativo, cuando la probabilidad de aceptación es 0,10 para ambos planes, se desvía menos del 5 % del valor λ de referencia del real decreto.
Esta condición se puede expresar de la siguiente forma4:
λ10i – λ10r | < 0.05 λ10r
A partir del gráfico o calculados a partir del cuadro C2, observamos que cuando la probabilidad del método de referencia es del 10 %, el valor λ es del 0,743. Se puede expresar como: λ10r=74,3 %
Siguiendo ahora la curva de eficacia del envasador, observamos que para una probabilidad del 10 % tenemos un valor λ = 1,059. Expresado en porcentaje: λ10i = 105,9 %
5. Aplicando la fórmula anterior:
| λ10i – λ10r | < 0.05 λ10r ➔ |105,9 – 74,3| < (0,05 · 74,3) ➔ 31,6 > 3,715 ➔ No cumple
El plan de muestreo del ejemplo C no es de eficacia comparable al realizado por el real decreto.
Ejemplo D.
En este último ejemplo utilizaremos un factor de riesgo 0,4 % para el envasador y una muestra por lote de 33 unidades.
| Plan de muestreo envasador: | β = 0,004 | α = 0,002 | 1-α = 0,998 |
| Plan de muestreo Real Decreto: | β = 0,01 | α = 0,005 | 1-α = 0,995 |
1. Las condiciones serán las siguientes:
CUADRO D1
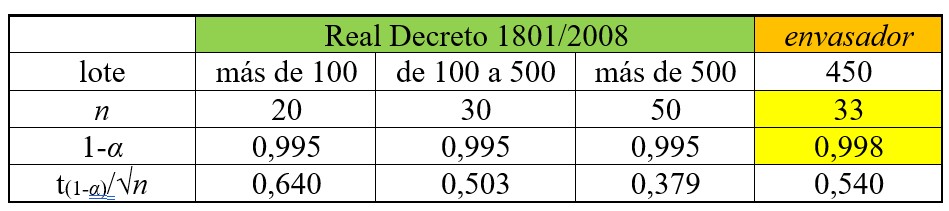
2. Si utilizamos la hoja de cálculo del ejercicio anterior, simplemente modificaremos las casillas amarillas del cuadro D1 y obtendremos directamente el cuadro de probabilidad de aceptación D2 y el gráfico correspondiente.
CUADRO D2
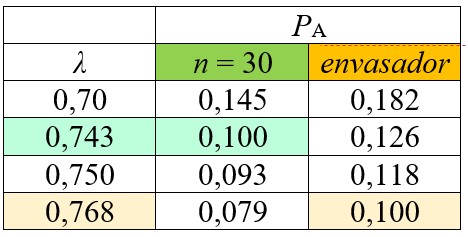
Figura 5.
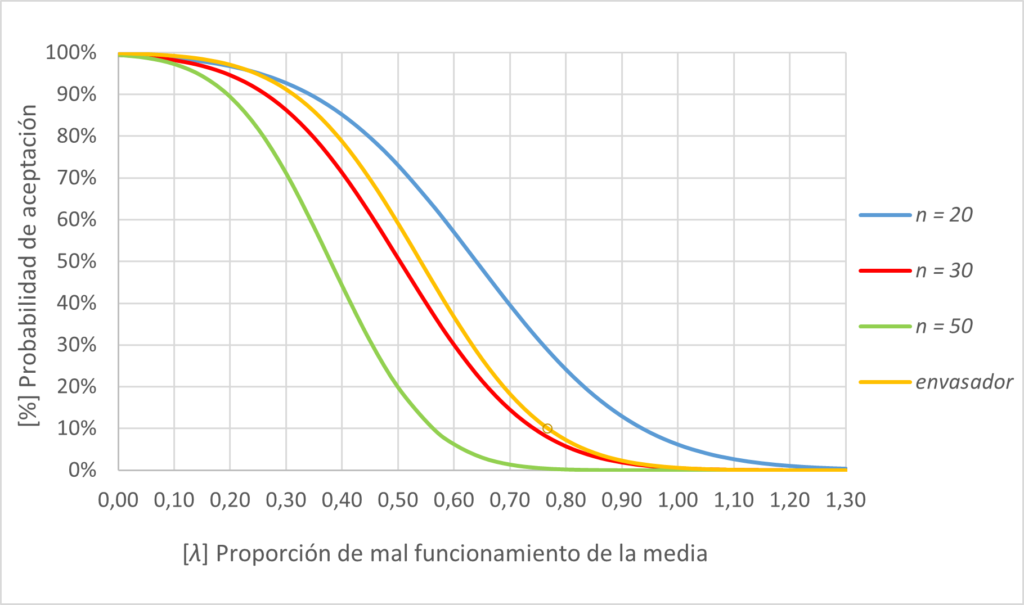
3. Obtendremos los valores lambda λ a partir del gráfico o calculados a partir del cuadro D2.
Para el método de referencia es el mismo del ejemplo C. λ10r =74,3 %
Para el método alternativo, con el nuevo nivel de confianza es λ10i = 76,8 %
4. Aplicando la fórmula anterior:
| λ10i – λ10r | < 0.05 · λ10r➔ |76,8 – 74,3|< (0,05 · 74,3) ➔2,5 < 3,715 ➔ Cumple
El plan de muestreo por variables del ejemplo D es de eficacia comparable al plan de muestreo por variables que realiza el real decreto.
5. Ahora podemos hallar el criterio de aceptación y rechazo para este plan de muestreo alternativo. Tal como indica el Real Decreto en el artículo 15.3, el valor de abscisa será:
\(\lambda=\left[\frac{\bar{Q_n}-\bar{x}}{s}\right]\)
Obtendremos el criterio de aceptación despejando x̄
Para aceptar el lote la media deberá cumplir la siguiente condición:
x̄ ≥ Qn – λ·s ➔ x̄ ≥ Qn – 0,54·s ;
donde:
x̄ = media calculada sobre la muestra;
Qn = cantidad nominal del envase;
s = desviación típica calculada sobre la muestra,
\(s = \sqrt{\sum_{i=1}^{i=n}\frac{\left(x_i-x^2\right)}{n-1}}\) ; donde:
xi = cantidad medida de cada envase de la muestra;
n = tamaño de muestra.
Conclusión:
Cuando se controla el contenido efectivo de los productos envasados, los servicios de inspección podrán solicitar la documentación en la que se consignen los resultados de dichos controles y ver si el procedimiento está organizado de tal manera que se pueda garantizar el valor del contenido nominal conforme las prescripciones del real decreto. Al controlar el contenido efectivo de los envases debemos diseñar un plan de muestreo idóneo. Podremos utilizar la hoja de cálculo de un ordenador y comparar la eficacia del nuevo plan de muestreo con el realizado por el real decreto. Podremos definir mejor las variables que afectan al control estadístico: el tamaño de los lotes, el tamaño de las muestras, los criterios de aceptación, el nivel de confianza y las funciones de cálculo de probabilidades. La calidad de nuestra fabricación, entendida como el ajuste de la cantidad envasada a la cantidad nominal que indica el envase, dependerá de otros factores, como la calidad de los envases vacíos, es decir la tara, la periodicidad de los controles, la proporción de envases con déficit de llenado, el error en servicio de los instrumentos de medida, factores humanos, entre otros. Comentar que el control del contenido efectivo es mejor cuando utilizamos instrumentos de pesaje de funcionamiento automático, con sistema de rechazo automático para los productos que tengan cierto déficit de llenado. Podremos así ajustar mejor la media del lote a la cantidad nominal deseada y guardar los registros de forma automática y será de mucha ayuda si envasamos con el marcaje CE “e”. También hay que tener en cuenta que, aunque tomar un gran tamaño de muestra pueda estimar mejor la calidad de nuestra producción, el coste adicional de inspeccionar una gran cantidad de piezas puede superar el beneficio derivado. Para ello, este artículo puede ser una ayuda al envasador, una herramienta más para poder mejorar la calidad de su producción y ajustarse a las normativas establecidas.
Bibliografía
[1] DIRECTIVA DEL CONSEJO de 20 de enero de 1976 relativa a la aproximación de las legislaciones de los Estados miembros sobre el preacondicionamiento en masa o en volumen de ciertos productos en envases previamente preparados. (76/211/CEE) (DO L 46 de 21.2.1976, p. 1). https://eur-lex.europa.eu/legal-content/EN/AUTO/?uri=CELEX:01976L0211-20190726
[2] Real Decreto 1801/2008, de 3 de noviembre, por el que se establecen normas relativas a las cantidades nominales para productos pre-envasados y al control de su contenido efectivo (BOE 266, de 04/11/2008). https://www.boe.es/diario_boe/txt.php?id=BOE-A-2008-17629
[3] DIRECTIVA 2007/45/CE DEL PARLAMENTO EUROPEO Y DEL CONSEJO de 5 de septiembre de 2007 por la que se establecen normas relativas a las cantidades nominales para productos preenvasados, se derogan las Directivas 75/106/CEE y 80/232/CEE del Consejo y se modifica la Directiva 76/211/CEE del Consejo. https://eur-lex.europa.eu/legal-ontent/ES/TXT/PDF/?uri=CELEX:32007L0045&from=es
[4] Revista e-medida nº 13, de marzo de 2018: “La idoneidad de los instrumentos de control utilizados por los envasadores en el etiquetado del contenido de productos envasados”. Antoni Alcaide i Gavilà. https://www.e-medida.es/numero-13/numero-13-la-idoneidad-de-los-instrumentos-de-control-utilizados-por-los-envasadores-en-el-etiquetado-del-contenido-de-productos-envasados/
[5] Orden ICT/155/2020, de 7 de febrero, por la que se regula el control metrológico del Estado de determinados instrumentos de medida. https://www.boe.es/diario_boe/txt.php?id=BOE-A-2020-2573
[6] Revista e-medida nº 6, de junio de 2014: “Diseño de una campaña de inspección de fábricas y plantas de envasado de productos envasados con cantidades nominales en unidades de masa”. Jorge Iñesta Burgos. https://www.e-medida.es/documentos/Numero-6/productos-envasados
[7] GUÍAS WELMEC
6.5 Orientación sobre los controles de los departamentos competentes en los productos envasados marcados con “℮”
6.7 Orientación para el control del mercado de los productos envasados para los departamentos competentes
https://www.welmec.org
[8] GUÍAS OIML
R.79 Requisitos para el etiquetado de productos envasados.
R. 87 Cantidad de producto dentro de los envases. Anexo F. Bases del modelo de muestreo estadístico utilizado.
https://www.oiml.org
Bibliografía relacionada
- Ley 32/2014, de 22 de diciembre, de Metrología (BOE 309, de 23/12/2014). https://www.boe.es/diario_boe/txt.php?id=BOE-A-2014-13359
- Real Decreto 244/2016, de 3 de junio, por el que se desarrolla la Ley 32/2014, de 22 de diciembre, de Metrología (BOE 137, de 07/06/2016). https://www.boe.es/diario_boe/txt.php?id=BOE-A-2016-5530
- UNE-ISO 2859-1. Procedimientos de muestreo para la inspección por atributos.
https://www.une.org/encuentra-tu-norma/busca-tu-norma/norma?c=N0049681
- Normativa aplicable a las cantidades nominales de productos envasados, publicado por Moisés Parejo Gómez en junio de 2018. https://www.comunidad.madrid/sites/default/files/doc/normativa_aplicable_productos_envasados.pdf
Notas al píe
1 La disposición adicional primera del Real Decreto 1801/2008, de 3 de noviembre, menciona que la utilización del símbolo CE «℮» establecida en el artículo 9.c) podrá autorizarse también cuando se utilicen métodos de control de eficacia comparable al recogido en la norma. Dichos métodos serán aprobados mediante la oportuna disposición de desarrollo de este real decreto. Hasta la fecha no se ha publicado ninguna disposición adicional al real decreto, por lo tanto, no existe esta opción. Si el envase lleva el etiquetado con el símbolo «℮», se deberán realizar los controles estadísticos de los artículos 11 y 12 del real decreto.
2 GUÍA WELMEC 6.7
APÉNDICE C: Equivalencia de los controles con la Directiva 76/2011
C. 2.1 Eficiencia del plan de muestreo único por atributos
3 GUÍA WELMEC 6.7
APÉNDICE C: Equivalencia de los controles con la Directiva 76/2011
C.2.2 Eficiencia del plan de muestreo doble por atributos
4 GUÍA WELMEC 6.7
A6 Comparar eficiencia de planes de muestreo.
A6a Prueba de atributos para comprobar la cantidad.
5 GUÍA WELMEC 6.7
APÉNDICE C: Equivalencia de los controles con la Directiva 76/2011
C 1 Características de los planes de muestreo para comprobar la media










Comentarios