Mª Dolores del Campo Maldonado
Centro Español de Metrología
Resumen:
La metrología ha evolucionado en el último siglo a la par con los desarrollos científicos y tecnológicos. Hay múltiples ejemplos del paso de grandes descubrimientos científicos, galardonados con premios Nobel, a su uso en metrología desde principios del siglo pasado: del interferómetro de Michelson hasta el uso del grafeno para el desarrollo de patrones eléctricos o el peine de frecuencia para la materialización del metro. Este artículo pretende resumir cómo la primera revolución cuántica en la segunda mitad del siglo pasado y la segunda revolución cuántica en estos momentos han contribuido y están contribuyendo al desarrollo de la metrología y de nuevos patrones de medida.
Palabras clave:
Metrología, física cuántica, efecto Josephson, efecto Hall cuántico, reloj óptico
Abstract:
Metrology has evolved in the last century along with scientific and technological developments. There are multiple examples of the use of great scientific discoveries, awarded with Nobel prizes, in metrology since the beginning of the last century: from the Michelson interferometer to the use of graphene for the development of electrical standards. This article aims to summarize how the first quantum revolution in the second half of the last century and the second quantum revolution at present have contributed and are contributing to the development of metrology and new measurement standards.
Key words:
Metrology, quantum physics, Josephson effect, Hall quantum effect, optical clock
1. Introducción
Cuando llevamos a cabo un proceso de medida para asignar un valor a una magnitud determinada necesitamos siempre establecer la unidad de medida. De acuerdo con el Vocabulario Internacional de Metrología (VIM) una unidad de medida es una magnitud escalar real, definida y adoptada por convenio, con la que se puede comparar cualquier otra magnitud de la misma naturaleza para expresar la relación entre ambas mediante un número. Esta otra magnitud es nuestra referencia o patrón y sin duda, la exactitud de nuestra medida nunca podrá ser mejor que la exactitud de nuestro patrón. Por ello, cuando desde la ciencia, la tecnología o la industria reclaman a la metrología unas mejores medidas, los metrólogos tenemos un único camino: mejorar nuestros patrones y procedimientos de medida.
Durante muchos años se ha trabajado en el desarrollo de patrones que sólo dependiesen de las constantes de la naturaleza y eso empujó a que el nuevo Sistema Internacional de Unidades [2] se apoyase en una serie de patrones cuánticos. En los siguientes apartados se presentarán los campos de la metrología en los que los fenómenos cuánticos clásicos como la segunda revolución cuántica están jugando un papel fundamental.
La primera revolución cuántica (fenómenos cuánticos clásicos) se basa en el carácter discreto de las magnitudes físicas como los estados o niveles de energía de los átomos. La segunda revolución cuántica se basa en el principio de superposición: un sistema se encuentra en todos sus posibles estados hasta que se realiza una medida sobre él.
2. Patrones eléctricos
Patrones de medida basados en fenómenos de la mecánica cuántica llevan siendo utilizados desde hace varias décadas, desde que Brian David Josephson recibió el Premio Nobel en 1973 por los estudios teóricos que predecían la cuantización del voltaje y Klaus von Klinzing en 1985 por el descubrimiento del efecto Hall cuántico. Esto supuso un cambio de paradigma para la metrología eléctrica ya que, hasta ese momento, la realización primaria del amperio, unidad del SI para la intensidad de corriente, se realizaba básicamente a través de la balanza de corriente que comparaba el peso de una masa con la fuerza magnética entre dos bobinas por las que circulaba una corriente eléctrica.
Josephson predijo que al irradiar un “sándwich” formado por dos superconductores separados por una fina capa de material aislante (el “queso”), lo que se conoce como una unión Josephson, con una señal de muy alta frecuencia (microondas) se producía una diferencia de tensión entre ambos cuantizada y proporcional a la frecuencia de microondas aplicadas ([3], [4]). Esto es debido a que parejas de electrones superconductores (pares de Cooper) pueden atravesar la barrera aislante de un superconductor al otro (efecto túnel). Y ¿cómo puede suceder esto? La razón está en las propiedades de los superconductores. Los metales son superconductores que a muy bajas temperatura (por debajo de su temperatura crítica) no presentan resistencia al flujo de corriente eléctrica. El motivo es que los electrones se emparejan formando los pares de Cooper, esto les permite caer en un estado de baja energía creando un “gap” de energía. Debido a este “gap” y a su baja energía los pares de Cooper se pueden mover por que los iones de la red no oponen resistencia (ver figura 1).
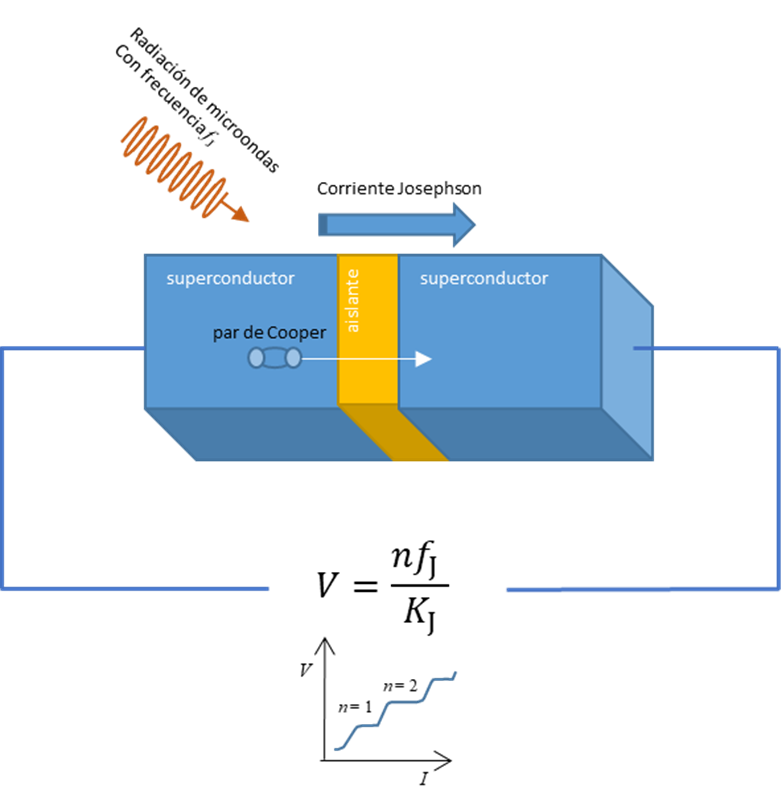
El hecho de que esta diferencia de potencial esté cuantizada, significa que se producen escalones (n) proporcionales a la constante de Josephson (KJ) y a la frecuencia de la radiación de microondas (fJ). Como \(K_J= \frac{h}{2e}\), esto significa que los valores de los escalones depende sólo de dos constantes fundamentales: la constante de Plank (h) y la carga del electrón (e) y de la frecuencia de microondas, que se puede medir con mucha exactitud (ver figura 1). Podemos entonces generar valores de tensión con muy poca incertidumbre, es decir: es un patrón ideal para el voltio.
Edwin Hall en 1879 observó que en una muestra sometida a un campo magnético trasversal por el que pasaba una corriente eléctrica se generaba un voltaje transversal: el voltaje Hall (figura 2). El principio subyacente es la fuerza de Lorentz, es decir, la fuerza sobre una carga puntual debida a campos electromagnéticos que son impulsadas transversalmente generando el voltaje Hall. . La famosa “regla del pulgar” permite determinar la dirección de la fuerza sobre un portador de carga según su dirección de movimiento y la dirección del campo magnético aplicado
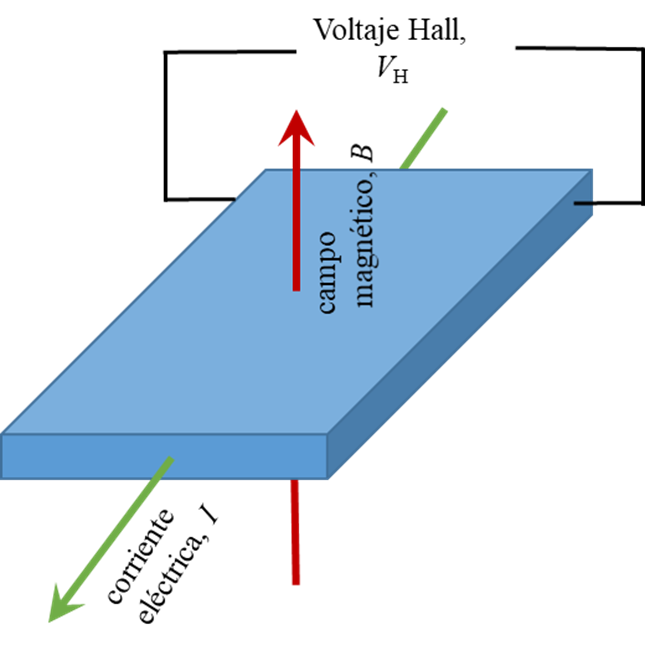
Klaus von Klitzing observó que si esta muestra era superconductora y bidimensional, si estaba a muy baja temperatura (1,4 K) y se sometía a grandes campos magnéticos, de varios teslas, al aplicar la corriente aparecían ciertas regiones en las que el voltaje Hall permanecía constante ante variaciones del campo magnético. Estas son las mesetas de resistencia Hall (RH) definidas como el cociente entre el voltaje Hall y la intensidad de corriente aplicada:
\(R_H= \frac{1}{i} \frac{h}{e^2} =\frac{R_{K}}{i} \:\:\: con\:\: i=1,2,…\)
A RK, que solo depende de constantes fundamentales se la conoce como constante de von Klitzing.
Este fenómeno permite por tanto el poder realizar patrones cuánticos de resistencia eléctrica.
Gracias a los efectos Hall y Josephson y a la simple ley de Ohm:
\(I=\frac{V}{R}\)
(1)
Se puede materializar, de acuerdo con el SI, la unidad de corriente eléctrica: el amperio [5].
3. Relojes atómicos
El campo eléctrico no es el único en metrología en el que la mecánica cuántica ha tenido un papel destacado. En 1955 Louis Essen, en el National Physical Laboratory (el instituto nacional de metrología de Reino Unido) construyó el primer reloj atómico de cesio.
En un reloj atómico de cesio, los átomos de cesio se canalizan por un tubo donde se someten a una radiación electromagnética con una frecuencia de 9 192 631 770 Hz (microondas), ni un hercio más ni uno menos. Los fotones asociados a esta radiación tienen exactamente una energía que es igual a la diferencia entre los dos niveles energéticos el estado fundamental del cesio. Los átomos de cesio absorben esta energía y cambian su estado. Un detector al final del tubo realiza un conteo del número de átomos que llegan y que han cambiado sus estados de energía. Cuanto más sintonizada esté la frecuencia de la radiación electromagnética al valor anterior, más átomos de cesio llegarán al detector. El detector entonces devuelve información a la fuente de microondas que la utiliza para sintonizarse con el número máximo de átomos de cesio. Otros componentes electrónicos del reloj atómico realizan el conteo de esta frecuencia [6].
Si comparamos un reloj atómico con un reloj de péndulo, la base para el conteo del tiempo, en vez de ser la oscilación de la masa se basa en las propiedades de los átomos cuando cambian de estado de energía.
En metrología de tiempo además del reloj de cesio se utiliza el máser de hidrógeno que se basa en la transición hiperfina de 1,4 GHz del átomo de hidrógeno. Éstos tienen una estabilidad a corto plazo mucho mejor que el cesio. Y claro, también se están utilizando en la actualidad los relojes ópticos, que se comentan brevemente en la siguiente sección.
4. Relojes ópticos
Cómo se ha explicado anteriormente la segunda revolución cuántica hace uso de las propiedades de entrelazamiento. En forma simple significa que cuando dos partículas están entrelazas cualquier propiedad de una de ellas está totalmente correlacionada con la otra, independientemente de la distancia que las separe. Estas partículas pueden ser, por ejemplo fotones o electrones y significa que cuando mides alguna propiedad de una de las partículas entrelazadas conoces inmediatamente el valor de la otra, aunque estén separadas por años luz.
Un reloj óptico, es un reloj atómico que utiliza frecuencias de transición en el rango óptico en vez de en el rango de microondas, lo que permite mejorar significativamente las incertidumbres de medida de los relojes de cesio, ya que las frecuencias ópticas son unos cinco órdenes de magnitud mayores que las de microondas. Se utilizan dos tipos de tecnología: uno o dos iones atrapados o átomos ultrafríos confinados en campos electromagnéticos en forma de redes ópticas.
Un reloj de iones basado en lógica cuántica es un ejemplo de cooperación entre dos iones donde cada uno proporciona cualidades complementarias. Por ejemplo, el ion del aluminio Al+ tiene una frecuencia de transición en el rango óptico que es útil para la frecuencia de referencia del reloj. Sin embargo, su estructura de niveles le hace un mal candidato para enfriarlo directamente a las temperaturas necesarias para estabilizarlo. En cambio, esto sí es posible con el ion de berilio Be+. Usando protocolos de computación cuántica, la información sobre el estado interno del ion espectroscópico Al+ después de sondear su transición con un láser, puede ser fielmente transferida al ion lógico Be+, en donde esta información puede ser detectada con eficiencia casi del 100% [9].
5. Medida de longitud
La mejora de las medidas ópticas en la segunda mitad del siglo pasado y las necesidades de mejoras en las exactitudes de la medida de longitud, en el año 1960 se pasó a definir el metro en base a la longitud de onda de la radiación de una transición particular del criptón 86. La idea subyacente era la misma que algo más tarde sirvió para redefinir el segundo: la transición electrónica en los átomos era un fenómeno inmutable de la naturaleza y como tal un patrón ideal para una magnitud física, en este caso la longitud. Gracias a la interferometría se podía medir la diferencia de camino óptico contando las franjas de interferencia (ver figura 3). Más adelante en 1983 se pasó a definir el metro a partir de la distancia que la luz recorría en el vacío en un tiempo igual a 1/c donde c es el valor de la velocidad de la luz.
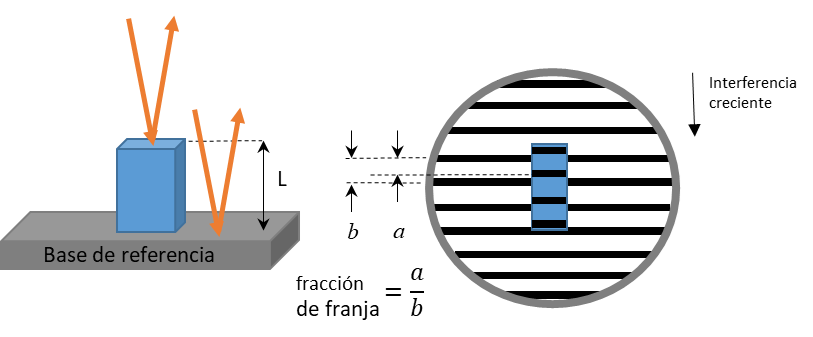
Esta nueva definición del metro impulsó el uso del láser en metrología dimensional ya que un láser emite luz monocromática, colimada y coherente. La radiación emitida tiene una única longitud de onda, todos sus fotones divergen mínimamente de su origen y pueden ser considerados paralelos y además en fase. La posibilidad de la fabricación de láseres fue una sugerencia de Albert Einstein que indicó que bajo las condiciones adecuadas, podían liberar su exceso de energía como luz, de forma espontánea o cuando son estimulados. El funcionamiento de los láser está determinado por las reglas de la mecánica cuántica: los átomos y las moléculas sólo pueden tener cantidades discretas de energía almacenada que depende de la naturaleza de átomo o la molécula. El nivel de energía más bajo para un átomo individual ocurre cuando todos sus electrones están en las órbitas más cercanas posibles a su núcleo. Esta condición se denomina estado fundamental. Cuando uno o más de los electrones de un átomo han absorbido energía, pueden moverse a órbitas exteriores, y entonces se dice que el átomo está “excitado”. Los estados excitados generalmente no son estables; a medida que los electrones caen de niveles de mayor energía a niveles de menor energía, emiten la energía adicional en forma de luz. Los fotones pueden ser emitidos de forma espontánea, pero también estimulada, por ejemplo iluminando el material del láser con una luz determinada o haciendo pasar una corriente eléctrica.
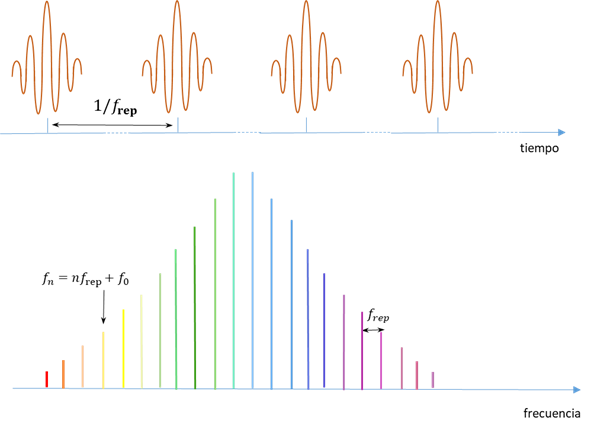
El uso del peine de frecuencias en metrología es otro caso en el que los últimos avances científicos fueron de aplicación inmediata en metrología. Un peine de frecuencias es una fuente laser, que gracias a que es ultrarrápida y emite pulsos ultracortos a ritmo regular, su espectro consiste en una serie de líneas de frecuencia discretas e igualmente espaciadas. Los peines de frecuencia óptica emiten un tren continuo de pulsos de luz muy breves y estrechamente espaciados que contienen todas las frecuencias posibles desde el infrarrojo invisible hasta el espectro visible y ultravioleta. Gracias a una técnica llamada “bloqueo de modo”, todas las frecuencias de cada pulso comienzan en fase, sincronizadas entre sí. El resultado se asemeja a los dientes de un peine, separando cada frecuencia en un pico distinto y la separación entre picos es muy pequeña y uniforme, lo que sirve para medir otras frecuencias con extrema precisión y exactitud.
6. La balanza de potencia
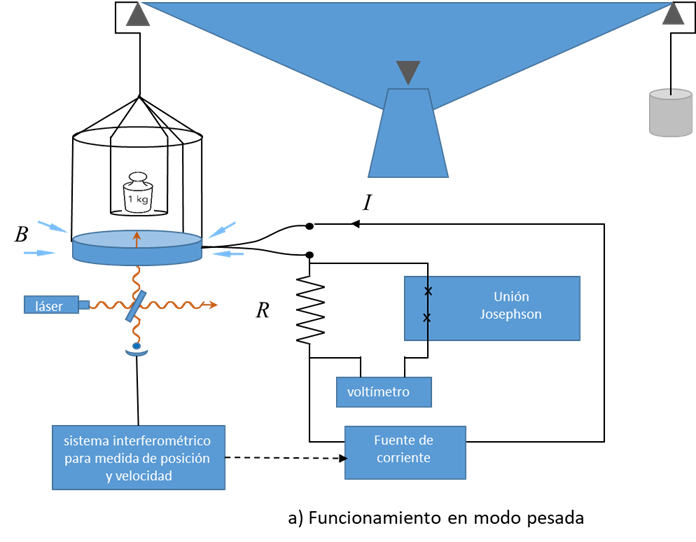
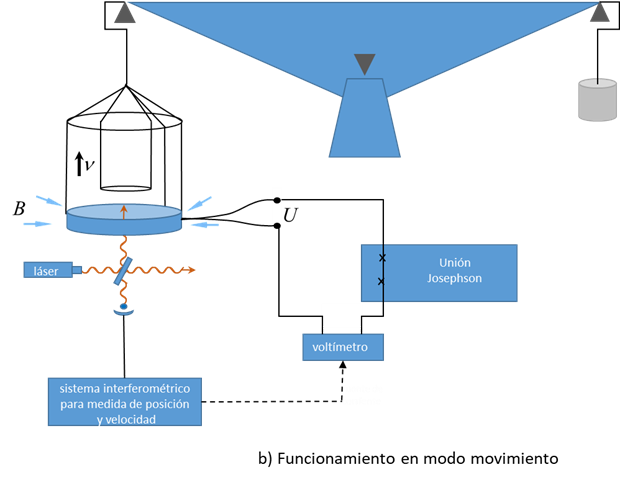
La nueva definición del kilogramo también se ha beneficiado de la física cuántica ya que se basa en fijar el valor numérico de la constante de Plank. Una de las formas de realizarlo es mediante la balanza de potencia o de Kibble [8].
En una balanza de Kibble se equilibra la fuerza gravitatoria de un cuerpo de masa m con la fuerza electromagnética que genera una bobina circular de longitud L por la que pasa una corriente eléctrica de intensidad I en el seno de un campo magnético radial de densidad de flujo B:
B L I = m g
Donde g es la fuerza de la gravedad. Para determinar el producto de B·l, que es muy difícil de determinar directamente, se induce en dicha bobina una fuerza electromotriz e y se desplaza dicha bobina con velocidad v, mediante un motor eléctrico y empleando sistemas interferométricos para medir la posición. Como resultado se tiene una ecuación con dimensiones de potencia, por lo que a veces a este método se le ha llamado también de la balanza de potencia:
m g ν = I Ɛ
La intensidad de corriente I se puede determinar como el cociente entre una tensión U y una resistencia R. Esta resistencia se puede medir en función de la constante de von Klitzing, RK, gracias al efecto Hall cuántico, mientras que las tensiones U y Ɛ se pueden medir en función de la contante de Josephson, KJ, utilizando el efecto del mismo nombre explicado en el apartado 2. La expresión anterior permite entonces determinar la masa en función de la constante de Planck h. La figura 5 muestra un esquema simplificado del funcionamiento
7. La candela cuántica
La candela cuántica aunque aún no se haya puesta en práctica puede ser una realidad gracias al desarrollo de las fuentes de fotones únicos que permitiría contar fotones con longitud de onda conocida. Como un fotón es un cuanto de energía que depende de su frecuencia, se podría correlacionar el número de fotones con una cantidad de energía o potencia determina. De esta forma, la candela pasaría a depender directamente de las constante de Plank, h, y de la velocidad de la luz, c.
8. Instrumentos de medida extremadamente sensible
Los principios fundamentales de la mecánica cuántica también han sido empleados para construir instrumentos de medida extremadamente sensibles como el SQUID (siglas de Superconducting Quantum Interference Device). En esencia un SQUID es un anillo superconductor con una o dos uniones Josephson entre medias.
La primera aplicación metrológica importante es como un detector de nulo por debajo de los femtovoltios, también son componentes básicos de los comparadores criogénicos de corriente CCC que se emplean para la medida de resistencia usando el efecto Hall. Pero también se utilizan en termómetros basados en la susceptibilidad magnética y en termómetros de ruido Johnson. Otro campo en el que se usan es en el de radiofrecuencia para medidas de atenuación [8].
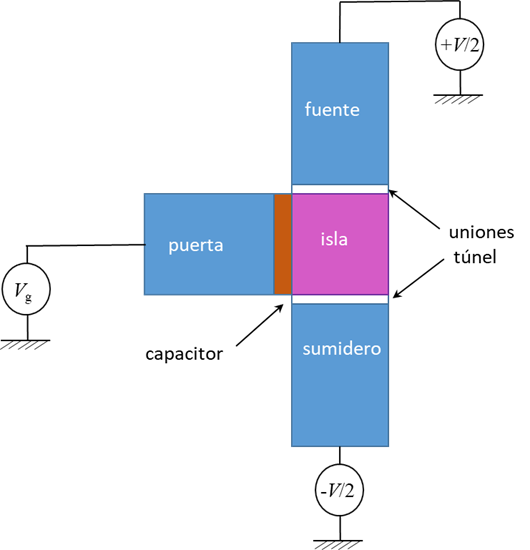
Otro ejemplo además del SQUID es el SET (siglas de Single-Electron Tunneling), que permite contar electrones de forma individual. Con una estructura similar a un transistor clásico, contiene en su interior una fuente de electrones, una “puerta” que controla el flujo y un sumidero por donde salen los electrones y son medidos. La diferencia es que un SET contiene una isla de silicio, entre dos uniones túnel, que permite manipular la corriente. Los electrones provenientes de la fuente se almacenan temporalmente en la isla usando otra puerta de voltaje. Mediante el control de los voltajes en las dos puertas, se puede conseguir que un solo electrón permanezca en la isla antes de pasar al sumidero. Repitiendo este proceso muchas veces y muy rápidamente, se consigue establecer una corriente de la que se pueden contar sus electrones [9]. La figura 6 presenta un esquema simplificado del SET.
9. Termómetros cuánticos
Los fenómenos cuánticos de segunda generación también son un nuevo camino para el desarrollo de termómetros primarios, es decir termómetros cuyo funcionamiento se basa en leyes de la física. Por ejemplo, las correlaciones cuánticas optomecánicas; mediante la combinación de dispositivos nano-fotónicos con sistemas nano-mecánicos se pueden construir patrones primarios cuánticos que usan la escala de energías cuánticas, determinada por la constante de Planck, para medir el movimiento térmico. Si se sondea un oscilador mecánico con un láser provoca cambios correlacionados en el movimiento del oscilador y en las propiedades de la luz transmitida, lo que permite utilizar el sistema como termómetro cuántico distinguiendo el movimiento óptico del mecánico (correlaciones fotón-fonón).
Referencias
[1] Vocabulario Internacional de Metrología: https://www.cem.es/sites/default/files/vim-cem-2012web.pdf
[2] Sistema Internacional de Unidades: https://www.cem.es/sites/default/files/30362_elsistemainternacionaldeunidades_web_0.pdf
[3] B. D. Josepshon, Possible New Effects in Superconductive Tunnelling. Phys. Rev. Lett. 1 (1962) 251.
[4] https://www.e-medida.es/numero-15/la-definicion-del-amperio-en-el-si-revisado/
[6] https://www.e-medida.es/numero-9/relojes-opticos/
[7] https://doi.org/10.1002/9783527609956.ch9
[8] https://www.e-medida.es/numero-14/2019-la-definicion-del-kilogramo-en-el-si-revisado/
[9] ¿Qué es el nuevo Sistema Internacional de Unidades de medida?, Dolores del Campo, Miguel Ángel Martin-Delgado. ISBN978-84-1352-367-5
User Review
( votes)Summary









Comentarios